本文實(shí)例為大家分享了python實(shí)現(xiàn)ANN的具體代碼，供大家參考，具體內(nèi)容如下

1.簡(jiǎn)要介紹神經(jīng)網(wǎng)絡(luò)

神經(jīng)網(wǎng)絡(luò)是具有適應(yīng)性的簡(jiǎn)單單元組成的廣泛并行互聯(lián)的網(wǎng)絡(luò)。它的組織能夠模擬生物神經(jīng)系統(tǒng)對(duì)真實(shí)世界物體做做出的反應(yīng)。神經(jīng)網(wǎng)絡(luò)的最基本的成分是神經(jīng)元模型，也就是最簡(jiǎn)單的神經(jīng)元模型。

“M-P模型”

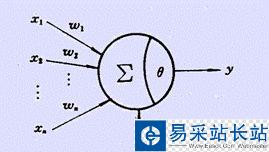
如上圖所示，神經(jīng)元接收到來(lái)自n個(gè)其他神經(jīng)元傳遞過(guò)來(lái)的輸入信號(hào)，這些信號(hào)通過(guò)帶權(quán)重的鏈接進(jìn)行傳遞。神經(jīng)元接收到的總輸入值將與神經(jīng)元的閾值進(jìn)行比較，然后通過(guò)“激活函數(shù)”處理以產(chǎn)生神經(jīng)元的輸出

激活函數(shù)：

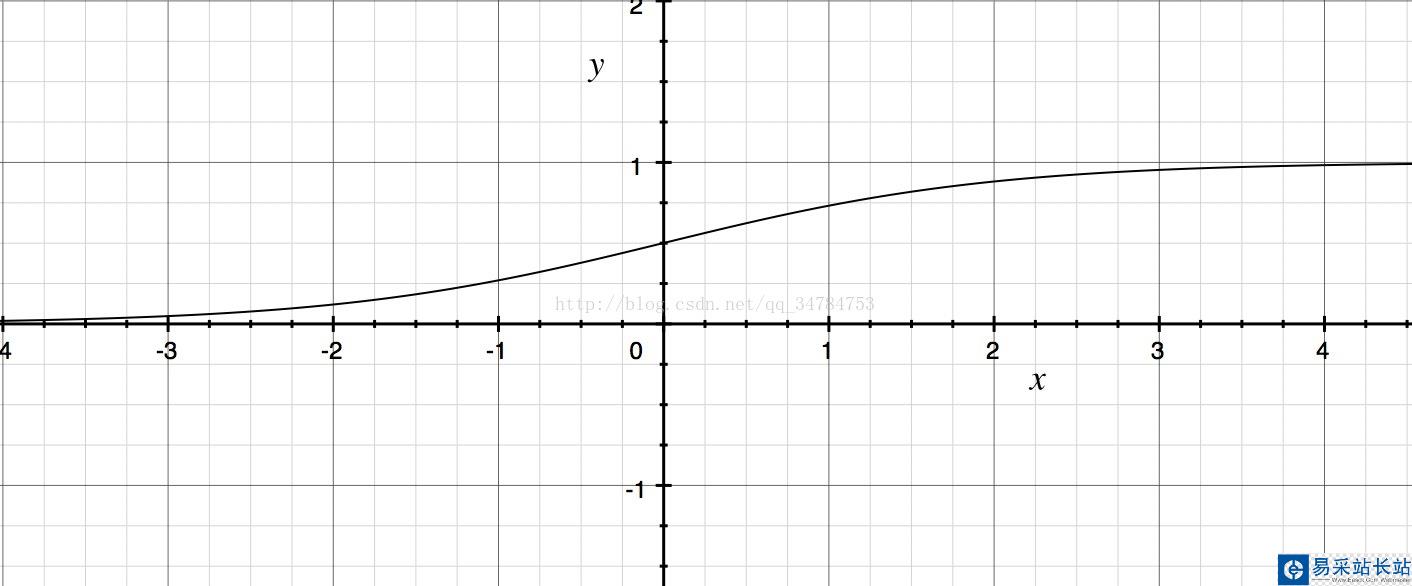
理想的激活函數(shù)應(yīng)該是階躍函數(shù)，也就是它能夠?qū)⑤斎胫涤成涑蔀檩敵鲋?或1。其中“0”代表神經(jīng)元抑制，“1”代表神經(jīng)元興奮。但是由于階躍函數(shù)不連續(xù)且不可導(dǎo)，因此實(shí)際上常常使用sigmoid函數(shù)當(dāng)做神經(jīng)元的激活函數(shù)。它能夠?qū)⒖赡茉谳^大范圍內(nèi)變化的輸出值擠壓到（0，1）之間這個(gè)范圍內(nèi)。因此有時(shí)也成為擠壓函數(shù)。常用的sigmoid函數(shù)是回歸函數(shù)

f(x) = 1/(1+e^(-x))

如下圖所示：

感知機(jī)：

感知機(jī)是最簡(jiǎn)單的神經(jīng)網(wǎng)絡(luò)，它由兩層神經(jīng)元組成。輸入層接受外界信號(hào)后傳遞給輸出層。輸出層是M-P神經(jīng)元。感知機(jī)也成為閾值邏輯單元。感知機(jī)可以通過(guò)采用監(jiān)督學(xué)習(xí)來(lái)逐步增強(qiáng)模式劃分的能力，達(dá)到學(xué)習(xí)的目的。

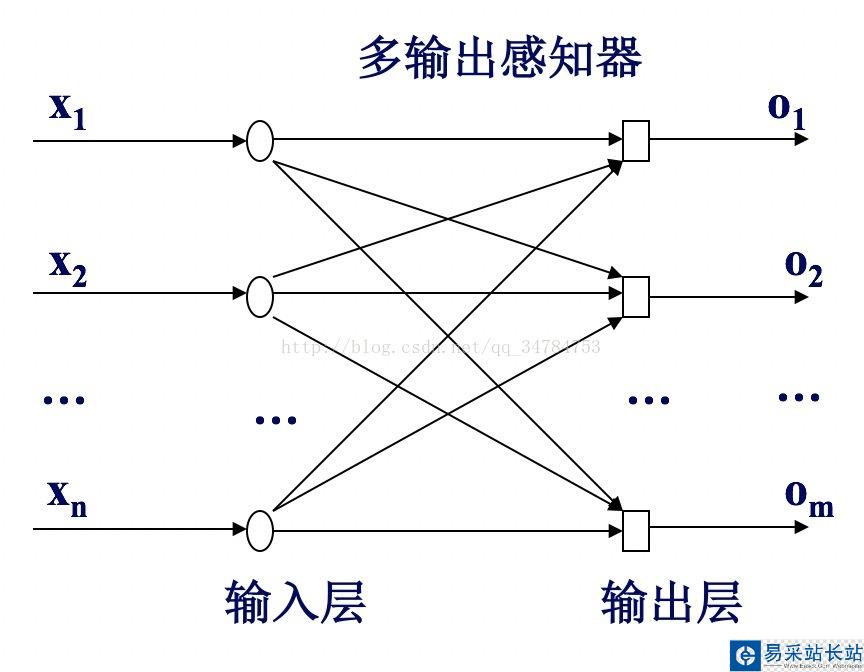
感知機(jī)能夠?qū)崿F(xiàn)簡(jiǎn)單的邏輯運(yùn)算。

一般的，對(duì)于給定訓(xùn)練數(shù)據(jù)集，權(quán)重Wi以及閾值θ可以通過(guò)學(xué)習(xí)得到。其中閾值(bias)可以通過(guò)學(xué)習(xí)得到。在輸出神經(jīng)元中，閾值可以看做是一個(gè)固定輸入為-1，0的啞結(jié)點(diǎn)，所對(duì)應(yīng)的連接權(quán)重為Wn+1，從而使得權(quán)重和閾值的學(xué)習(xí)統(tǒng)一為權(quán)重的學(xué)習(xí)。

感知機(jī)的學(xué)習(xí)規(guī)則非常簡(jiǎn)單，對(duì)于訓(xùn)練樣本（X，y），若當(dāng)前感知機(jī)輸出為y',則感知機(jī)做如下調(diào)整

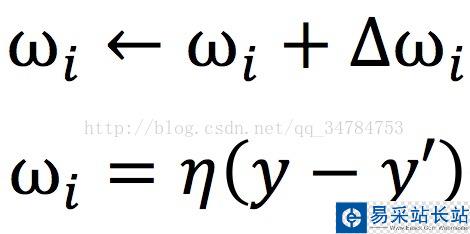
其中，η屬于（0，1）,稱為“學(xué)習(xí)率”

若感知機(jī)對(duì)訓(xùn)練樣例預(yù)測(cè)正確，則感知機(jī)不發(fā)生變化，否則將根據(jù)錯(cuò)誤的程度進(jìn)行權(quán)重的調(diào)整。

需要注意的是，感知機(jī)只有輸出神經(jīng)元進(jìn)行激活函數(shù)處理，因此它的學(xué)習(xí)能力非常有限，也就是因?yàn)樗挥幸粚庸δ苌窠?jīng)元。

可以證明，若兩類模式實(shí)現(xiàn)性可分的，即存在一個(gè)超平面可以將他們分開(kāi)，則利用感知機(jī)一定會(huì)收斂，可以求得一個(gè)權(quán)向量。否則，感知機(jī)的學(xué)習(xí)過(guò)程將會(huì)發(fā)生震蕩，導(dǎo)致參數(shù)難以穩(wěn)定下來(lái)，不等求得合適的解。例如，單層感知機(jī)不能解決抑或問(wèn)題。