寫在最前
在之前的這篇文章中我們提到了對于貝塞爾公式的運用。本次分享一下如何推導貝塞爾公式以及附一個簡單的🌰即小球跟隨曲線軌跡運動。
效果預覽
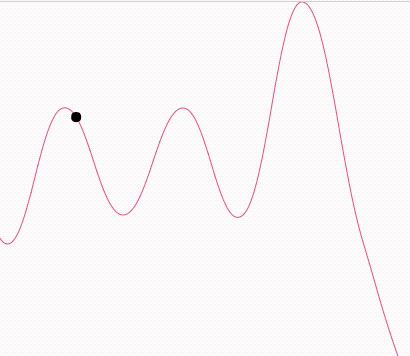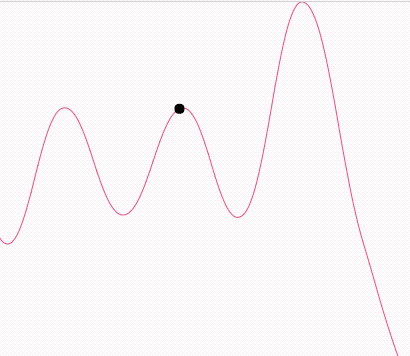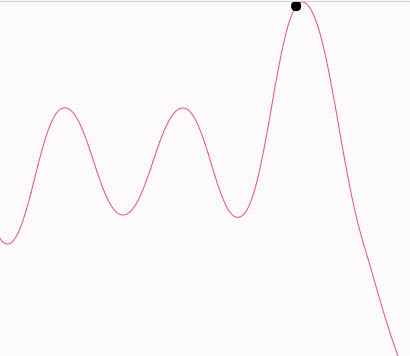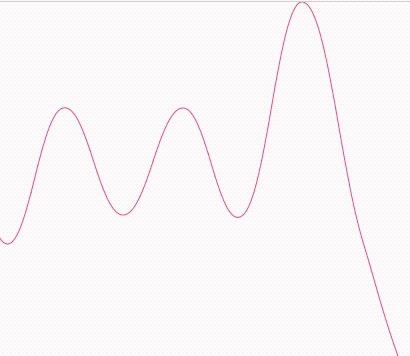
demo地址
對于如何繪制連續的貝塞爾曲線可以參照這篇文章:基于canvas使用貝塞爾曲線平滑擬合折線段
在本例中生成的曲線由以上文章中的源碼提供。
貝塞爾曲線公式推導

上面這張圖是貝塞爾曲線的完整公式,看起來一臉懵逼=。=,因為這是N階的推導公式,本次我們以一二階貝塞爾公式的推導來理解一下這個推導公式的由來。先來看下網上流傳已久的幾張貝塞爾動圖:



在這三張圖中最重要的部分是我們需要理解變量t。t的取值范圍是0-1。從上面的gif中也可以看出來似乎曲線的繪制過程就是t從0到1的過程。嗯其實就是這樣的。t的真實含義是什么呢?
在p0p1、p1p2、p2p3等等的起點到控制點再到終點的連線中,每段連線都被分割成了兩部分(仔細看動圖中的黑色、綠色、藍色圓點),各段連線中兩部分的比值都是相同的,比值范圍是0到1,而這個比值就是t
來看下面的一階貝塞爾曲線示意圖:

pt是p0p1上的任意一點,p0pt / ptp1 = t。從而我們可以引出下面的推導

此時t為時間,v為速度。我們可以看做從p0到p1的距離等于固定速度乘以固定時間

故到p上某一點的時間為固定的速度乘以某個時間值。同時固定的速度已經已經可以表示為上面的推導公式。此時等式右邊就形成了t(0,1) / t;即相當于某個時間值 / 固定時間值,即產生了我們一開始所強調的變量t,其取值范圍為[0,1]。從而下面的等式也就比較好理解了。

至此一階貝塞爾曲線我們已經推到了出來,其中變量為起點、終點與比值t。
那么二階公式如何從一階過渡過去呢?
來看下面這張圖:

其中Pp(t)的經過路徑就是我們所求的二階貝塞爾曲線,那么其實我們也可以將其從一階進行演變:

我們先將pa、pb兩個點所連線段當做一階曲線,之后再由兩端一階曲線分別表示pa、pb,最后就得到了我們的二階曲線公式。仔細觀察就能發現這和我們最初的完整公式是相同的:

其中n選擇不同數值時就可以得出不同階的曲線公式。同時從上面的推導過程也可以知道,不論是幾階曲線,我們都可以完全由一階來表示,而這個“表示”的過程就是我們在上面看到的形成動畫中那些輔助線。故可以感受下作者自己寫的曲線形成動畫中的效果,每段輔助線均由一階曲線形成:

相關地址
物體跟隨復雜曲線軌跡運動
當我們知道曲線的公式有何而來之后,如何讓小球沿著曲線運動就很好理解了。我們生成的每段曲線都是可以用公式表示出來的,也正因如此我們就可以得到每個t值時的曲線坐標點。從而知道物體的繪制坐標。
//核心邏輯LinearGradient.prototype.drawBall = function() { var self = this var item = ctrlNodesArr[ctrlDrawIndex] //存儲了各段曲線的控制點 //各段曲線均為三階貝塞爾,故下面計算x,y值代入到了三階公式中 var ctrlAx = item.cAx,//各個控制點 ctrlAy = item.cAy, ctrlBx = item.cBx, ctrlBy = item.cBy, ... if(item.t > 1) { ctrlDrawIndex++ //當一段曲線的t>1說明曲線已經走到頭 }else { self.ctx.clearRect(0, 0, self.width, self.height) item.t += 0.05 var ballX = ox * Math.pow((1 - item.t), 3) + 3 * ctrlAx * item.t * Math.pow((1 - item.t), 2) + 3 * ctrlBx * Math.pow(item.t, 2) * (1 - item.t) + x * Math.pow(item.t, 3) var ballY = oy * Math.pow((1 - item.t), 3) + 3 * ctrlAy * item.t * Math.pow((1 - item.t), 2) + 3 * ctrlBy * Math.pow(item.t, 2) * (1 - item.t) + y * Math.pow(item.t, 3) //代入三階貝塞爾曲線公式算出小球的坐標值 self.ctx.beginPath() self.ctx.arc(ballX, ballY, 5, 0, Math.PI * 2, false) self.ctx.fill() } if(ctrlDrawIndex !== ctrlNodesArr.length) { window.requestAnimationFrame(newMap.drawBall.bind(self)) }}最后
demo地址:這里✨✨
源碼地址:歡迎star
以上就是本文的全部內容,希望對大家的學習有所幫助,也希望大家多多支持武林網。
新聞熱點
疑難解答