寫在最前
本次分享一下在canvas中將繪制出來的折線段的棱角“磨平”,也就是通過貝塞爾曲線穿過各個描點來代替原有的折線圖。
為什么要平滑擬合折線段
先來看下Echarts下折線圖的渲染效果:
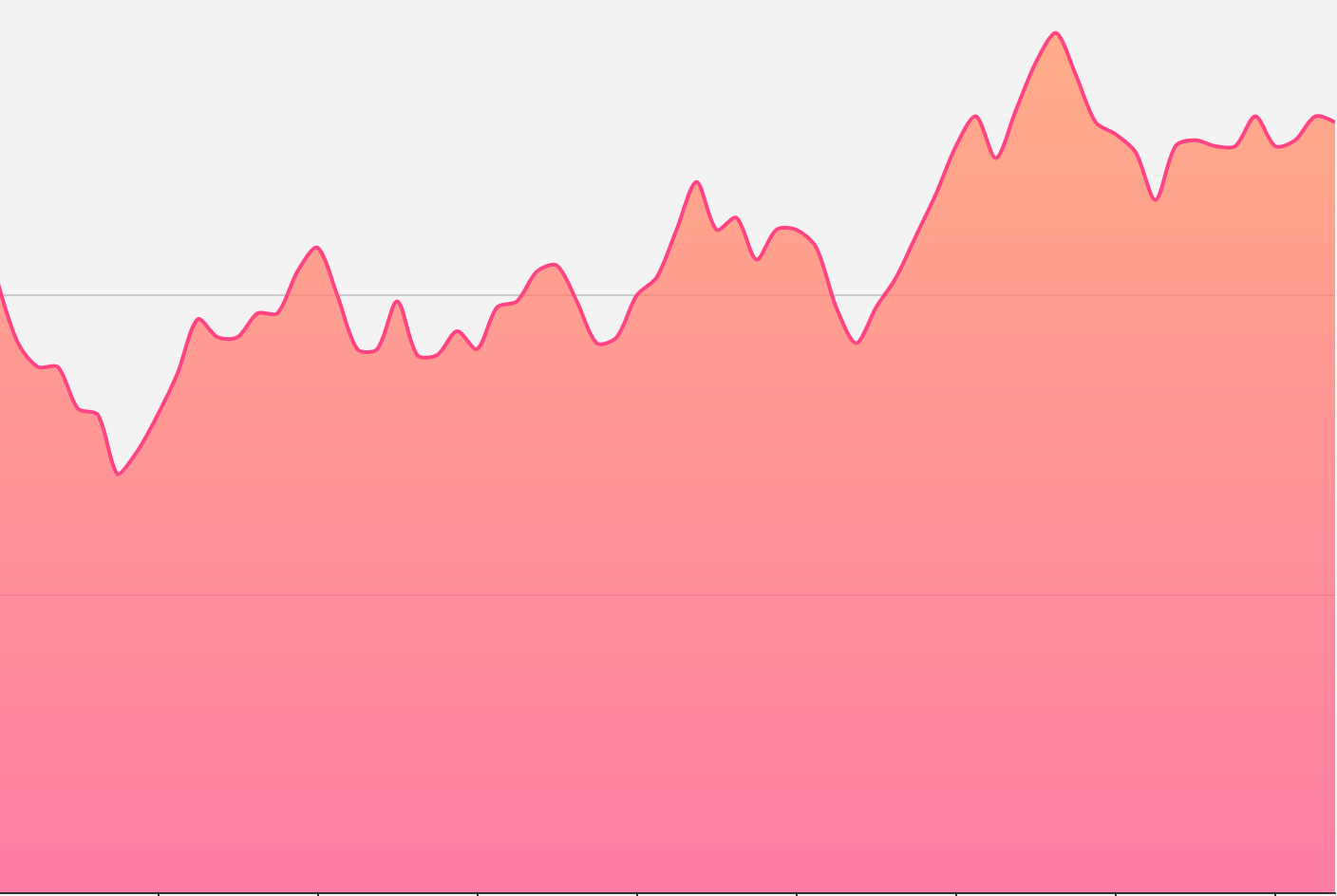
一開始我沒注意到其實這個折線段是曲線穿過去的,只認為是單純的描點繪圖,所以起初我實現的“簡(丑)易(陋)”版本是這樣的:
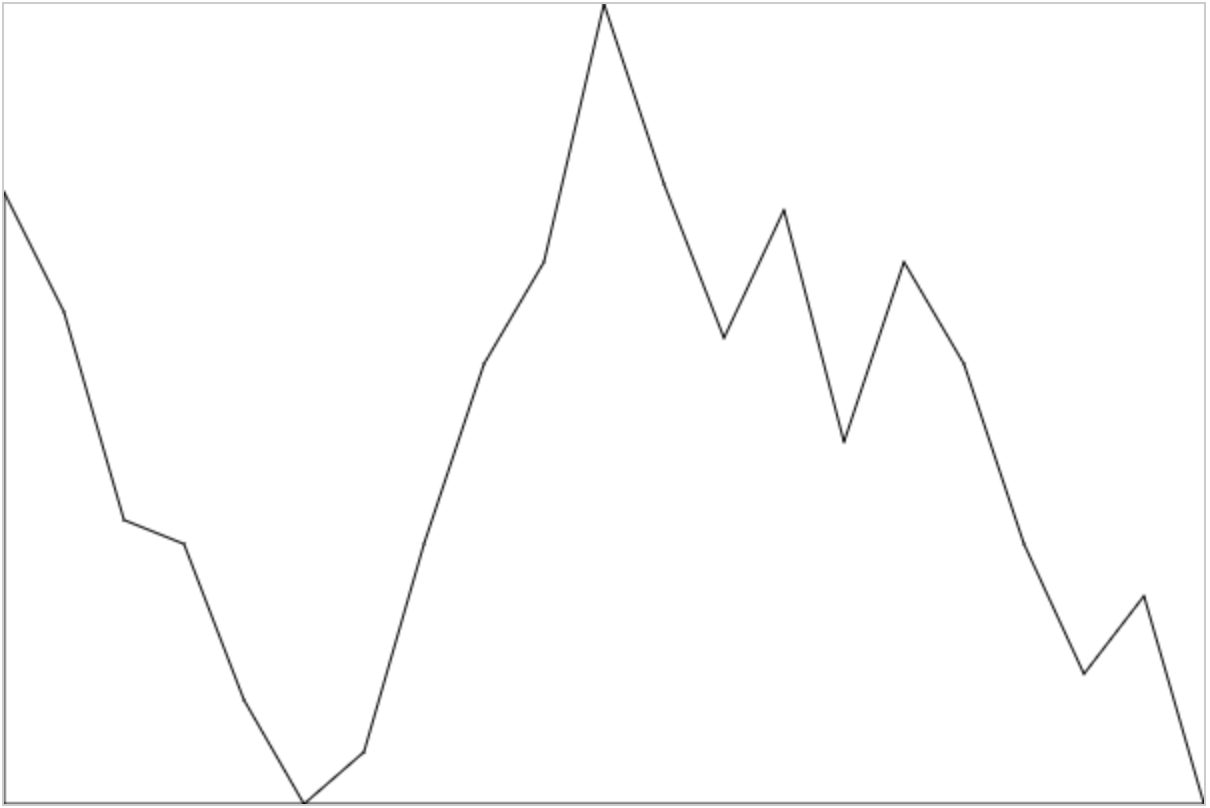
不要關注樣式,重點就是實現之后才發現看起來人家Echarts的實現描點非常的圓滑,也由此引發了之后的探討。怎么有規律的畫平滑曲線?
效果圖
先來看下最終模仿的實現:
因為我也不知道Echarts內部怎么實現的(逃
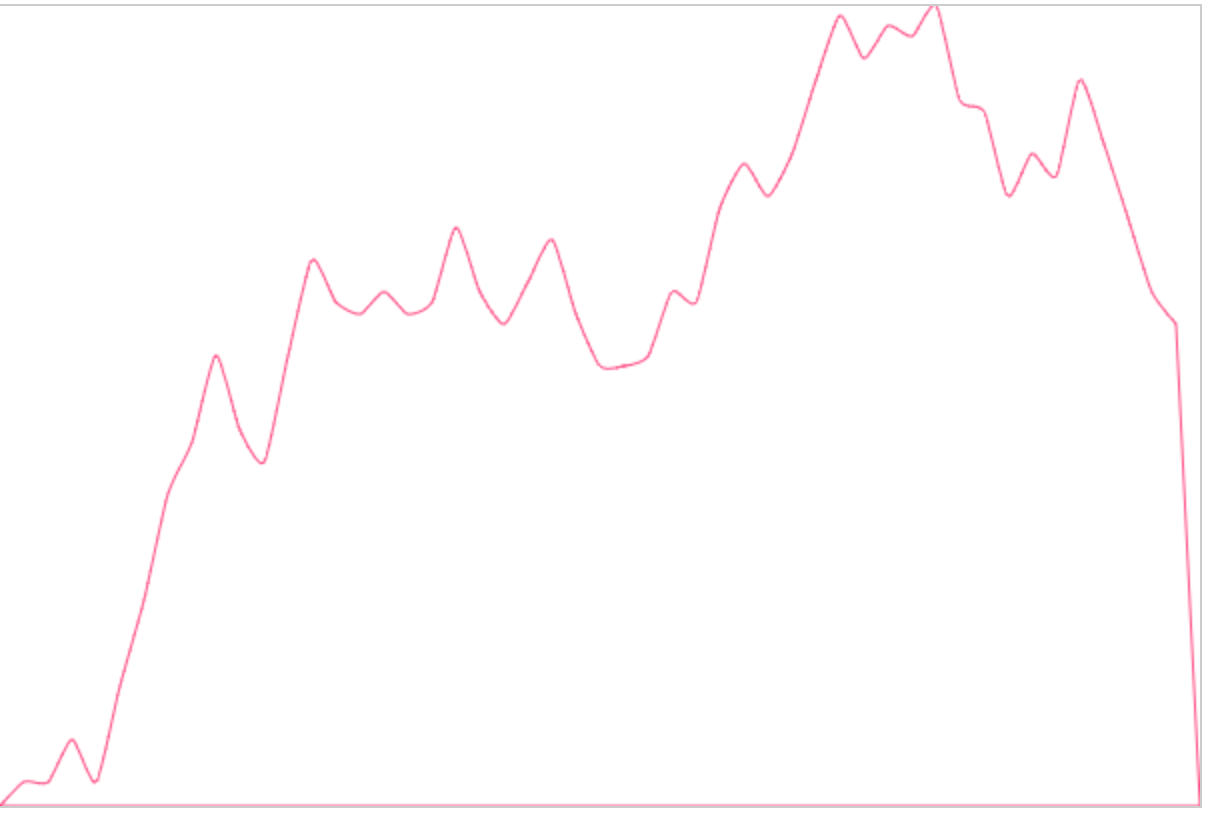
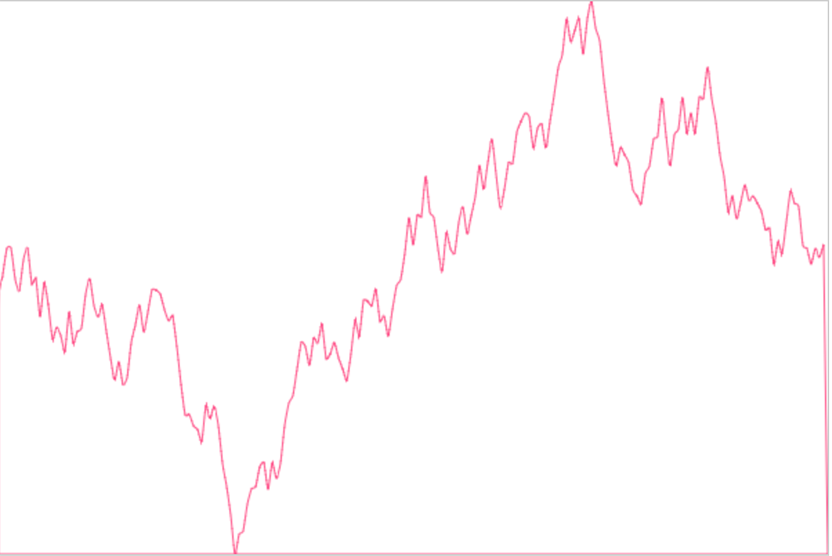
看起來已經非常圓潤了,和我們最初的設想十分接近了。再看下曲線是否穿過了描點:
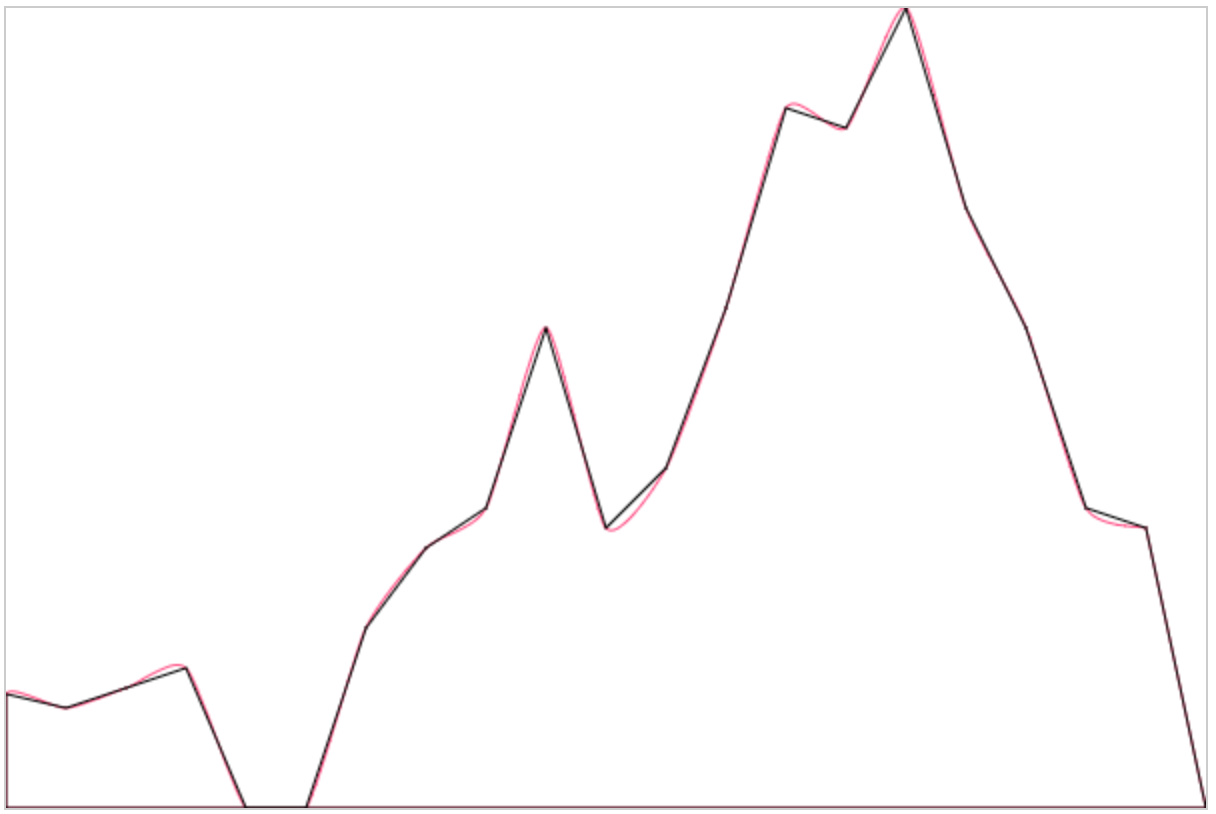
好的!結果很明顯現在來重新看下我們的實現方式。
實現過程
模擬數據
var data = [Math.random() * 300]; for (var i = 1; i < 50; i++) { //按照echarts data.push(Math.round((Math.random() - 0.5) * 20 + data[i - 1])); } option = { canvas:{ id: 'canvas' }, series: { name: '模擬數據', itemStyle: { color: 'rgb(255, 70, 131)' }, areaStyle: { color: 'rgb(255, 158, 68)' }, data: data } };繪制折線圖
首先初始化一個構造函數來放置需要用到的數據:
function LinearGradient(option) { this.canvas = document.getElementById(option.canvas.id) this.ctx = this.canvas.getContext('2d') this.width = this.canvas.width this.height = this.canvas.height this.tooltip = option.tooltip this.title = option.text this.series = option.series //存放模擬數據}繪制折線圖:
LinearGradient.prototype.draw1 = function() { //折線參考線 ... //要考慮到canvas中的原點是左上角, //所以下面要做一些換算, //diff為x,y軸被數據最大值和最小值的取值范圍所平分的等份。 this.series.data.forEach(function(item, index) { var x = diffX * index, y = Math.floor(self.height - diffY * (item - dataMin)) self.ctx.lineTo(x, y) //繪制各個數據點 }) ...}貝塞爾曲線平滑擬合
貝塞爾曲線的關鍵點在于控制點的選擇,這個網站可以動態的展現控制點不同而繪制的不同的曲線。而對于控制點的計算。。作者還是選擇了百度一下畢竟數學不好:)。具體算法有興趣的同學可以深入了解下,現在直接說下計算控制點的結論。
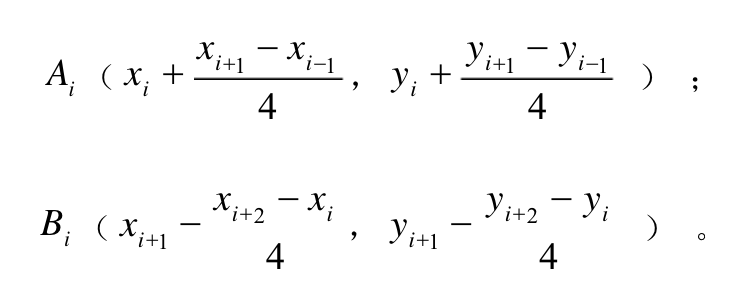
上面的公式涉及到四個坐標點,當前點,前一個點以及后兩個點,而當坐標值為下圖展示的時候繪制出來的曲線如下所示:
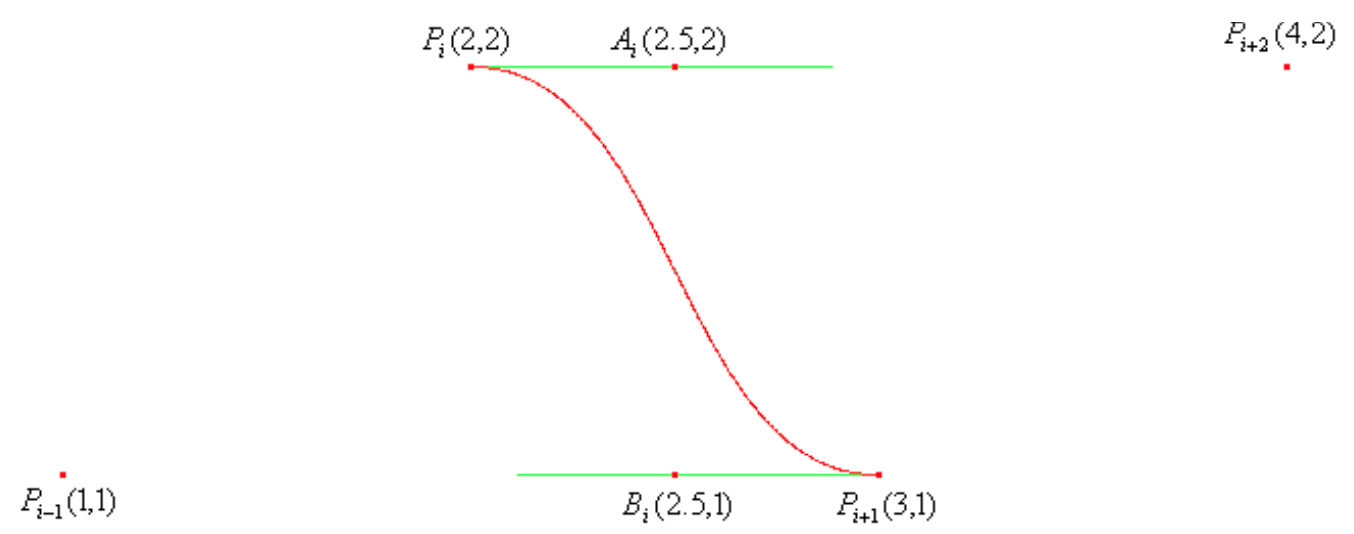
不過會有一個問題就是起始點和最后一個點不能用這個公式,不過那篇文章也給出了邊界值的處理辦法:

所以在將折線換成平滑曲線的時候,將邊界值以及其他控制點計算好之后代入到貝塞爾函數中就完成了:
//核心實現this.series.data.forEach(function(item, index) { //找到前一個點到下一個點中間的控制點 var scale = 0.1 //分別對于ab控制點的一個正數,可以分別自行調整 var last1X = diffX * (index - 1), last1Y = Math.floor(self.height - diffY * (self.series.data[index - 1] - dataMin)), //前一個點坐標 last2X = diffX * (index - 2), last2Y = Math.floor(self.height - diffY * (self.series.data[index - 2] - dataMin)), //前兩個點坐標 nowX = diffX * (index), nowY = Math.floor(self.height - diffY * (self.series.data[index] - dataMin)), //當期點坐標 nextX = diffX * (index + 1), nextY = Math.floor(self.height - diffY * (self.series.data[index + 1] - dataMin)), //下一個點坐標 cAx = last1X + (nowX - last2X) * scale, cAy = last1Y + (nowY - last2Y) * scale, cBx = nowX - (nextX - last1X) * scale, cBy = nowY - (nextY - last1Y) * scale if(index === 0) { self.ctx.lineTo(nowX, nowY) return } else if(index ===1) { cAx = last1X + (nowX - 0) * scale cAy = last1Y + (nowY - self.height) * scale } else if(index === self.series.data.length - 1) { cBx = nowX - (nowX - last1X) * scale cBy = nowY - (nowY - last1Y) * scale } self.ctx.bezierCurveTo(cAx, cAy, cBx, cBy, nowX, nowY); //繪制出上一個點到當前點的貝塞爾曲線 })由于我每次遍歷的點都是當前點,但是文章中給出的公式是計算會知道下一個點的控制點算法,故在代碼實現中我將所有點的計算挪前了一位。當index = 0時也就是初始點是不需要曲線繪制的,因為我們繪制的是從前一個點到當前點的曲線,沒有到0的曲線需要繪制。從index = 1開始我們就可以正常開始繪制,從0到1的曲線,由于index = 1時是沒有在他前面第二個點的故其屬于邊界值點,也就是需要特殊進行計算,以及最后一個點。其余均按照正常公式算出AB的xy坐標代入貝塞爾函數即可。
最后
源代碼見這里
以上就是本文的全部內容,希望對大家的學習有所幫助,也希望大家多多支持武林網。
新聞熱點
疑難解答