一、貝葉斯分類介紹

貝葉斯分類器是一個(gè)統(tǒng)計(jì)分類器。它們能夠預(yù)測(cè)類別所屬的概率，如：一個(gè)數(shù)據(jù)對(duì)象屬于某個(gè)類別的概率。貝葉斯分類器是基于貝葉斯定理而構(gòu)造出來的。對(duì)分類方法進(jìn)行比較的有關(guān)研究結(jié)果表明：簡單貝葉斯分類器（稱為基本貝葉斯分類器）在分類性能上與決策樹和神經(jīng)網(wǎng)絡(luò)都是可比的。在處理大規(guī)模數(shù)據(jù)庫時(shí)，貝葉斯分類器已表現(xiàn)出較高的分類準(zhǔn)確性和運(yùn)算性能。基本貝葉斯分類器假設(shè)一個(gè)指定類別中各屬性的取值是相互獨(dú)立的。這一假設(shè)也被稱為：類別條件獨(dú)立，它可以幫助有效減少在構(gòu)造貝葉斯分類器時(shí)所需要進(jìn)行的計(jì)算。

二、貝葉斯定理

p(A|B) 條件概率 表示在B發(fā)生的前提下，A發(fā)生的概率；

基本貝葉斯分類器通常都假設(shè)各類別是相互獨(dú)立的，即各屬性的取值是相互獨(dú)立的。對(duì)于特定的類別且其各屬性相互獨(dú)立，就會(huì)有：

 P(AB|C) = P(A|C)*P(B|C)

三、貝葉斯分類案例

1.分類屬性是離散

假設(shè)有樣本數(shù)為6個(gè)的訓(xùn)練集數(shù)字如下：

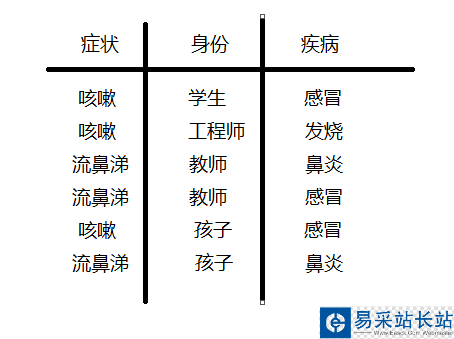
現(xiàn)在假設(shè)來又來了一個(gè)人是癥狀為咳嗽的教師，那這位教師是患上感冒、發(fā)燒、鼻炎的概率分別是多少呢？這個(gè)問題可以用貝葉斯分類來解決，最后三個(gè)疾病哪個(gè)概率高，就把這個(gè)咳嗽的教師劃為哪個(gè)類,實(shí)質(zhì)就是分別求p(感冒|咳嗽*教師)和P(發(fā)燒 | 咳嗽 * 教師)

P(鼻炎 | 咳嗽 * 教師) 的概率；

假設(shè)各個(gè)類別相互獨(dú)立：

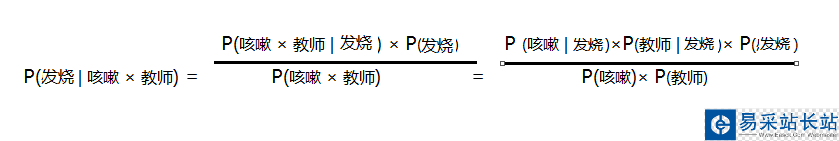
 P(感冒)=3/6    P(發(fā)燒)=1/6     P(鼻炎)=2/6

 p(咳嗽) = 3/6   P(教師）= 2/6

 p(咳嗽 | 感冒) = 2/3   P(教師 | 感冒) = 1/3

故

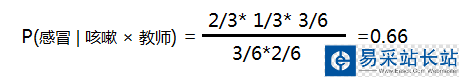
按以上方法可分別求  P(發(fā)燒 | 咳嗽 × 教師) 和P(鼻炎 |咳嗽 × 教師 )的概率；

2.分類屬性連續(xù)

如果按上面的樣本上加一個(gè)年齡的屬性；因?yàn)槟挲g是連續(xù)，不能采用離散變量的方法計(jì)算概率。而且由于樣本太少，所以也無法分成區(qū)間計(jì)算；這時(shí)，可以假設(shè)感冒、發(fā)燒、鼻炎分類的年齡都是正態(tài)分布，通過樣本計(jì)算出均值和方差，也就是得到正態(tài)分布的密度函數(shù)；

下面就以求P(年齡=15|感冒)下的概率為例說明：

   第一：求在感冒類下的年齡平均值  u=(15+48+12)/3=25