做機(jī)器學(xué)習(xí)的一定對(duì)支持向量機(jī)（support vector machine-SVM）頗為熟悉，因?yàn)樵谏疃葘W(xué)習(xí)出現(xiàn)之前，SVM一直霸占著機(jī)器學(xué)習(xí)老大哥的位子。他的理論很優(yōu)美，各種變種改進(jìn)版本也很多，比如latent-SVM, structural-SVM等。這節(jié)先來(lái)看看SVM的理論吧，在（圖一）中A圖表示有兩類的數(shù)據(jù)集，圖B,C,D都提供了一個(gè)線性分類器來(lái)對(duì)數(shù)據(jù)進(jìn)行分類？但是哪個(gè)效果好一些？

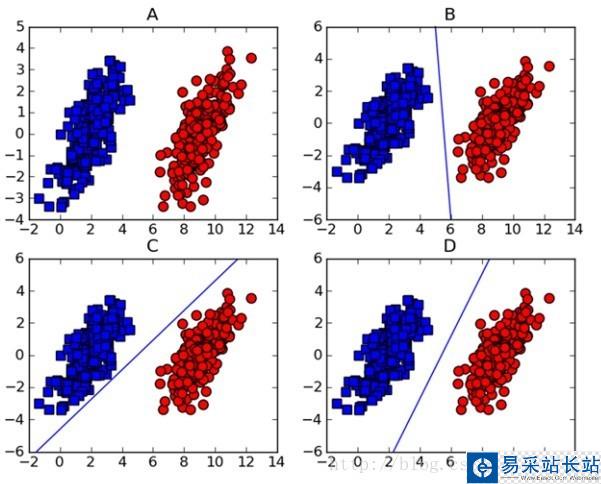
（圖一）

        可能對(duì)這個(gè)數(shù)據(jù)集來(lái)說(shuō)，三個(gè)的分類器都一樣足夠好了吧，但是其實(shí)不然，這個(gè)只是訓(xùn)練集，現(xiàn)實(shí)測(cè)試的樣本分布可能會(huì)比較散一些，各種可能都有，為了應(yīng)對(duì)這種情況，我們要做的就是盡可能的使得線性分類器離兩個(gè)數(shù)據(jù)集都盡可能的遠(yuǎn)，因?yàn)檫@樣就會(huì)減少現(xiàn)實(shí)測(cè)試樣本越過(guò)分類器的風(fēng)險(xiǎn)，提高檢測(cè)精度。這種使得數(shù)據(jù)集到分類器之間的間距（margin）最大化的思想就是支持向量機(jī)的核心思想，而離分類器距離最近的樣本成為支持向量。既然知道了我們的目標(biāo)就是為了尋找最大邊距，怎么尋找支持向量？如何實(shí)現(xiàn)？下面以（圖二）來(lái)說(shuō)明如何完成這些工作。

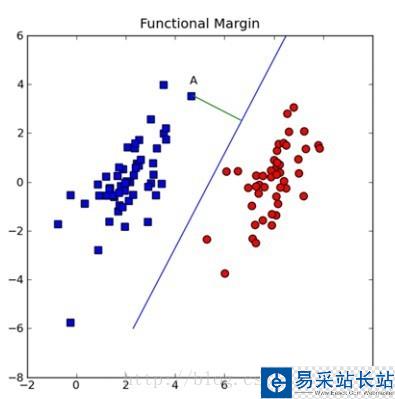
（圖二）

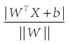假設(shè)（圖二）中的直線表示一個(gè)超面，為了方面觀看顯示成一維直線，特征都是超面維度加一維度的，圖中也可以看出，特征是二維，而分類器是一維的。如果特征是三維的，分類器就是一個(gè)平面。假設(shè)超面的解析式為，那么點(diǎn)A到超面的距離為,下面給出這個(gè)距離證明：

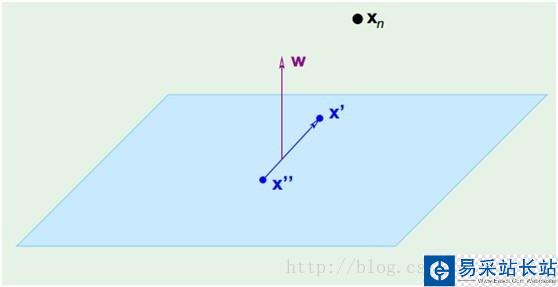
（圖三）

在（圖三）中，青色菱形表示超面，Xn為數(shù)據(jù)集中一點(diǎn)，W是超面權(quán)重，而且W是垂直于超面的。證明垂直很簡(jiǎn)單，假設(shè)X'和X''都是超面上的一點(diǎn)，

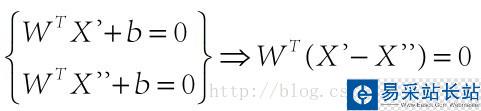
因此W垂直于超面。知道了W垂直于超面，那么Xn到超面的距離其實(shí)就是Xn和超面上任意一點(diǎn)x的連線在W上的投影，如（圖四）所示：

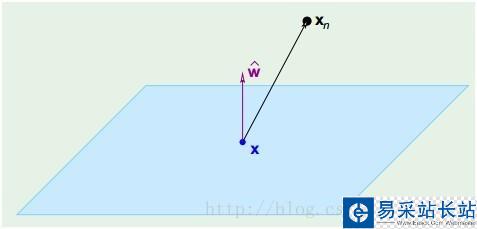
套進(jìn)拉格朗日乘子法公式得到如（公式五）所示的樣子：

（公式五）

        在（公式五）中通過(guò)拉格朗日乘子法函數(shù)分別對(duì)W和b求導(dǎo)，為了得到極值點(diǎn)，令導(dǎo)數(shù)為0，得到