這篇文章并不是介紹排序算法原理的，純粹是想比較一下各種排序算法在真實(shí)場(chǎng)景下的運(yùn)行速度。

算法由 Python 實(shí)現(xiàn)，可能會(huì)和其他語(yǔ)言有些區(qū)別，僅當(dāng)參考就好。

測(cè)試的數(shù)據(jù)是自動(dòng)生成的，以數(shù)組形式保存到文件中，保證數(shù)據(jù)源的一致性。

排序算法

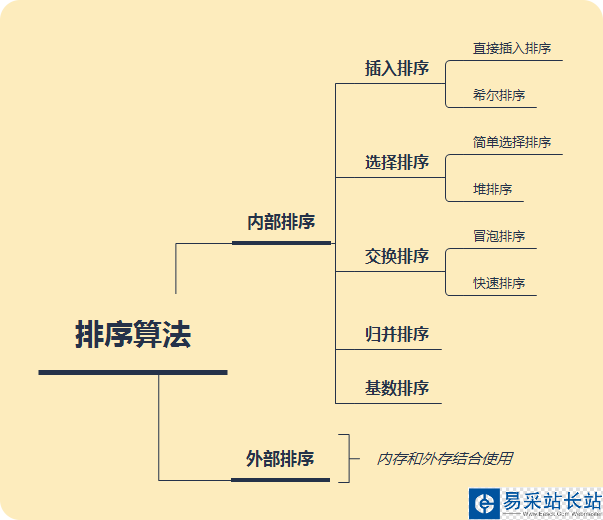
直接插入排序

時(shí)間復(fù)雜度：O(n²)
空間復(fù)雜度：O(1)
穩(wěn)定性：穩(wěn)定

def insert_sort(array):  for i in range(len(array)):    for j in range(i):      if array[i] < array[j]:        array.insert(j, array.pop(i))        break  return array

希爾排序

時(shí)間復(fù)雜度：O(n)
空間復(fù)雜度：O(n√n)
穩(wěn)定性：不穩(wěn)定

def shell_sort(array):  gap = len(array)  while gap > 1:    gap = gap // 2    for i in range(gap, len(array)):      for j in range(i % gap, i, gap):        if array[i] < array[j]:          array[i], array[j] = array[j], array[i]  return array

簡(jiǎn)單選擇排序

時(shí)間復(fù)雜度：O(n²)
空間復(fù)雜度：O(1)
穩(wěn)定性：不穩(wěn)定

def select_sort(array):  for i in range(len(array)):    x = i # min index    for j in range(i, len(array)):      if array[j] < array[x]:        x = j    array[i], array[x] = array[x], array[i]  return array

堆排序

時(shí)間復(fù)雜度：O(nlog₂n)
空間復(fù)雜度：O(1)
穩(wěn)定性：不穩(wěn)定

def heap_sort(array):  def heap_adjust(parent):    child = 2 * parent + 1 # left child    while child < len(heap):      if child + 1 < len(heap):        if heap[child + 1] > heap[child]:          child += 1 # right child      if heap[parent] >= heap[child]:        break      heap[parent], heap[child] = /        heap[child], heap[parent]      parent, child = child, 2 * child + 1  heap, array = array.copy(), []  for i in range(len(heap) // 2, -1, -1):    heap_adjust(i)  while len(heap) != 0:    heap[0], heap[-1] = heap[-1], heap[0]    array.insert(0, heap.pop())    heap_adjust(0)  return array

冒泡排序

時(shí)間復(fù)雜度：O(n²)
空間復(fù)雜度：O(1)
穩(wěn)定性：穩(wěn)定

def bubble_sort(array):  for i in range(len(array)):    for j in range(i, len(array)):      if array[i] > array[j]:        array[i], array[j] = array[j], array[i]  return array

快速排序

時(shí)間復(fù)雜度：O(nlog₂n)
空間復(fù)雜度：O(nlog₂n)
穩(wěn)定性：不穩(wěn)定

def quick_sort(array):  def recursive(begin, end):    if begin > end:      return    l, r = begin, end    pivot = array[l]    while l < r:      while l < r and array[r] > pivot:        r -= 1      while l < r and array[l] <= pivot:        l += 1      array[l], array[r] = array[r], array[l]    array[l], array[begin] = pivot, array[l]    recursive(begin, l - 1)    recursive(r + 1, end)  recursive(0, len(array) - 1)  return array