本教程向朋友們介紹MAYA表達(dá)式控制動(dòng)力學(xué)動(dòng)畫(huà)之小雞搶食場(chǎng)景的方法,群體動(dòng)畫(huà)是表達(dá)式或MAYA mel語(yǔ)言的強(qiáng)項(xiàng),下面我們來(lái)做一個(gè)追逐的表達(dá)式練習(xí),感興趣的朋友可以看看。
用小雞搶食的情景來(lái)說(shuō)明。
一群小雞在覓食,突然一只小雞發(fā)現(xiàn)一只小蟲(chóng),其他小雞過(guò)來(lái)?yè)屖常谑蔷蜁?huì)出現(xiàn)一群小雞追逐一只小雞的場(chǎng)景,在具體的測(cè)試中,我用一個(gè)球體代表叼著小蟲(chóng)的小雞,其他的小雞用圓錐表示。下面詳細(xì)說(shuō)明整個(gè)制作過(guò)程。
1.首先制作場(chǎng)景,建立一塊崎嶇不平的地面,代表小雞的球體和圓錐。如圖。
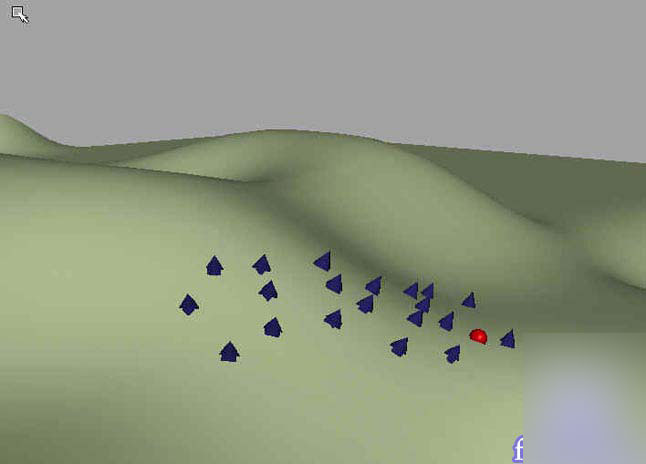
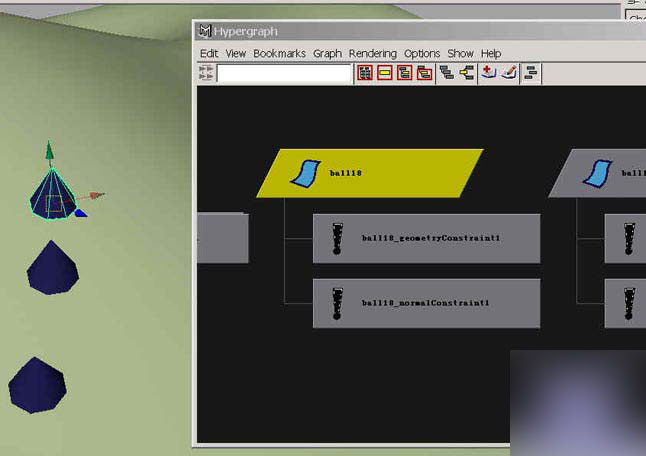
2.隨機(jī)的在地面上排布 "小雞"。.為了上小雞們能夠貼在地面并且是隨著地面坡度而發(fā)生相應(yīng)的角度傾斜,將小雞們與地面進(jìn)行法
線約束和幾何體約束,如圖。
4.打開(kāi)表達(dá)式編輯窗口,定義各小雞初始位置。
for($k=1;$k<41;$k=$k 1)
{
if(frame==1)
{$tx[0]=ball.translateX;//
$tx[1]=ball1.translateX=7.9;
$tx[2]=ball2.translateX=3;
$tx[3]=ball3.translateX=-0.8;
$tx[4]=ball4.translateX=1.3;
$tx[5]=ball5.translateX=-2;
$tx[6]=ball6.translateX=-4.3;
$tx[7]=ball7.translateX=8.8;
$tx[8]=ball8.translateX=16.02;
$tx[9]=ball9.translateX=12.0;
$tx[10]=ball10.translateX=5.2;
$tx[11]=ball1.translateX=-7.9;
$tx[12]=ball2.translateX=13;
$tx[13]=ball3.translateX=-10.8;
$tx[14]=ball4.translateX=21.3;
$tx[15]=ball5.translateX=-12;
$tx[16]=ball6.translateX=-14.3;
$tx[17]=ball7.translateX=28.8;
$tx[18]=ball8.translateX=10.02;
$tx[19]=ball9.translateX=18.0;
$tx[20]=ball10.translateX=15.2; $tz[0]=ball.translateZ;
$tz[1]=ball1.translateZ=1;
$tz[2]=ball2.translateZ=3.347;
$tz[3]=ball3.translateZ=8.908;
$tz[4]=ball4.translateZ=0.736;
$tz[5]=ball5.translateZ=2.525;
$tz[6]=ball6.translateZ=-2.145;
$tz[7]=ball7.translateZ=4.207;
$tz[8]=ball8.translateZ=0.542;
$tz[9]=ball9.translateZ=6.277;
$tz[10]=ball10.translateZ=5;
$tz[11]=ball11.translateZ=-1;
$tz[12]=ball12.translateZ=-3.347;
$tz[13]=ball13.translateZ=-8.908;
$tz[14]=ball14.translateZ=-0.736;
$tz[15]=ball15.translateZ=-2.525;
$tz[16]=ball16.translateZ=-10.145;
$tz[17]=ball17.translateZ=-4.207;
$tz[18]=ball18.translateZ=-5.542;
$tz[19]=ball19.translateZ=16.277;
$tz[20]=ball20.translateZ=15;
具體定義值根據(jù)當(dāng)時(shí)各小雞法線和幾何體約束后其位移通道的參數(shù)來(lái)定義,需要一些耐心,如果小雞更多的話,需要耐心更多,我知道我的方法很笨。有朋友知道簡(jiǎn)單方便的定義方式嗎?
5.下面進(jìn)行核心的算法說(shuō)明,在追逐中,不管小雞當(dāng)時(shí)在什么方位,他們的目標(biāo)都為有蟲(chóng)的小雞,另外小雞不能相互穿過(guò),所以在后面的小雞若要躍過(guò)前面的小雞,需要改變奔跑的方向,找空當(dāng)穿插追逐。
for($j=1;$j<41;$j=$j 1) {$dz[$j]=$tz[$j]-$tz[0];
$sign[$k]=sign($vz[$k])*sign($tz[$k]-$tz[$j]);
$dx[$j]=abs($tx[$j]-$tx[$k]);
if((abs($dz[$k]-$dz[$j])<5)
&&($sign[$k]>0)&&($dx[$j]<=5))
{ $lz[$k]=abs($dz[$k]-$dz[$j]);
$lz[$k]=min($lz[$k],$zz[$k]);
$zz[$k]=$lz[$k]; $code[$k]=$j;
$n[$k]=$n[$k] 1; }
}
這段程序是避免小雞們相互穿插的,通過(guò)判斷各小雞相對(duì)其它小雞的位置及距離,決定其加速或減速或改道。在這個(gè)練習(xí)中,我定義的小雞個(gè)體半徑為1個(gè)單位,所以我定義小雞前面若5個(gè)單位內(nèi)有其他小雞,它會(huì)考慮改變速度或方向。
if((abs($dz[$k]-$dz[$j])<5)
&&($sign[$k]>0)&&($dx[$j]<=5))
其中$lz[$k]是用來(lái)表示小雞前其他小雞在z軸方向相對(duì)其最近的距離。$n[$k]表示在同一幀中,某小雞前面(z軸方向)其他小雞距其距離小于5單位的個(gè)數(shù)。以上是用按照序號(hào)逐個(gè)小雞遍歷方式比較得出結(jié)果,因此在小雞數(shù)量較多或小雞速度較快時(shí),會(huì)有較大的誤差,有朋友知道根本解決問(wèn)題的方法嗎?
if($n[$k]==0)
$aFz[$k]=15 0*abs($dz[$k]/3);
else
$aFz[$k]=15 0*abs($dz[$k]/3)-$k1*(7-$lz[$k]);
if($tz[$k]<$tz[0])
$aFz[$k]=-$aFz[$k];
if(($lz[$k]<3)&&($n[$k]>0))
$afz[$k]=8*$k2*$vz[$k] 10*sign($vz[$k]);
else
$afz[$k]=$k2*$vz[$k];
$az[$k]=$aFz[$k]-$afz[$k];
if(($lz[$k]<2)&&($n[$k]>0))
$vz[$k]=$vz[$code[$k]];
else
$vz[$k]=$vz[$k] $az[$k]*$t; $tz[$k]=-$vz[$k]*$t-0.5*$az[$k]*$t*$t $tz[$k];
這段是定義各小雞在z軸方向奔跑加速度和速度及位置的程序。其中$aFz[$k]表示其他小雞相對(duì)有蟲(chóng)小雞的主動(dòng)加速度,$afz[$k]表示其他小雞在奔跑中因速度和前面障礙而產(chǎn)生的反向阻礙其追逐的加速度。
if(($lz[$k]<2)&&($n[$k]>0))
$vz[$k]=$vz[$code[$k]];
其中的這句表示如果某小雞前面有小雞與之距離小于2個(gè)單位時(shí),強(qiáng)制其速度與前面的這只小雞相同,從而避免穿插。另外式中的一些系數(shù)和參數(shù)大多是試驗(yàn)確定的,并不是最合理的定義。
$lx[$k]=$tx[$k]-$tx[$code[$k]];
$dx[$k]=$tx[$k]-$tx[0];
$aFx[$k]=-3*($dx[$k]/5) 0.05*sign($dx[$k]);
if(($lx[$k]<2)&&($n[$k]>0)&&($lz[$k]<2))
{$afx[$k]=-5*sign($lx[$k])*((2.5-$lx[$k])/2)*((2.5-$lx[$k])/2) $k3*$vx[$k];
$ax[$k]=0;}
else if(($n[$k]>0)&&($lz[$k]>=2))
$afx[$k]=-0.1*sign($lx[$k])*((5-$lx[$k])/2) $k3*$vx[$k];
else
$afx[$k]=$k3*$vx[$k];
$ax[$k]=$aFx[$k]-$afx[$k];
$vx[$k]=$vx[$k] $ax[$k]*$t;
$tx[$k]=$tx[$k] $vx[$k]*$t 0.5*$ax[$k]*$t*$t;
這段是定義各小雞在x軸方向奔跑加速度和速度及位置的程序。各變量含義與前類似。
最后,給各小雞的實(shí)體進(jìn)行賦值,如下:
ball.translateX=$tx[0];
ball1.translateX=$tx[1];
ball2.translateX=$tx[2];
ball3.translateX=$tx[3];
ball4.translateX=$tx[4];
ball5.translateX=$tx[5];
ball6.translateX=$tx[6];
ball7.translateX=$tx[7];
ball8.translateX=$tx[8];
ball9.translateX=$tx[9];
ball10.translateX=$tx[10];
ball11.translateX=$tx[11];
ball12.translateX=$tx[12];
ball13.translateX=$tx[13];
ball14.translateX=$tx[14];
ball15.translateX=$tx[15];
ball16.translateX=$tx[16];
ball17.translateX=$tx[17];
ball18.translateX=$tx[18];
ball19.translateX=$tx[19];
ball20.translateX=$tx[20]; ball1.translateZ=$tz[1];
ball2.translateZ=$tz[2];
ball3.translateZ=$tz[3];
ball4.translateZ=$tz[4];
ball5.translateZ=$tz[5];
ball6.translateZ=$tz[6];
ball7.translateZ=$tz[7];
ball8.translateZ=$tz[8];
ball9.translateZ=$tz[9];
ball10.translateZ=$tz[10];
ball11.translateZ=$tz[11];
ball12.translateZ=$tz[12];
ball13.translateZ=$tz[13];
ball14.translateZ=$tz[14];
ball15.translateZ=$tz[15];
ball16.translateZ=$tz[16];
ball17.translateZ=$tz[17];
ball18.translateZ=$tz[18];
ball19.translateZ=$tz[19];
ball20.translateZ=$tz[20];
同時(shí)還可以打印一些具體參量以便分析檢查小雞們的運(yùn)動(dòng)情況。
print("l:" $lx[2] " " $lx[5] " " $lx[10]
" n:" $n[1] ", " $n[2] ", " $n[3] ", " $n[4] ", " $n[5] ", " $n[6] ", " $n[7] ", " $n[8] ", " $n[10] "/n"
" dx:" $dx[2] " " $dx[5] " " $dx[10] "/n"
" aFx:" $aFx[2] " " $aFx[5] " " $aFx[10] "/n"
" ax:" $ax[2] " " $ax[5] " " $ax[10] " " "/n"
" afx:" $afx[2] " " $afx[5] " " $afx[10] "/n"
" vx:" $vx[2] " " $vx[5] " " $vx[10] "/n"
" tx:" $tx[2] " " $tx[5] " " $tx[10] "/n");
最后給出全部表達(dá)式的程序,供參考。
global float $tx[],$tz[],$dx[],$dz[],$lx[],$lz[],$vx[],
$vz[],$aFx[],$afx[],$aFz[],$afz[],$ax[],$az[],$t=0.053,
$sign[],$zx[],$zz[],$k1=0.5,$k2=0.5,$k3=2,$k4;
int $code[],$i,$j,$k,$m,$n[]; for($k=1;$k<41;$k=$k 1)
{
if(frame==1)
{$tx[0]=ball.translateX;//
$tx[1]=ball1.translateX=7.9;
$tx[2]=ball2.translateX=3;
$tx[3]=ball3.translateX=-0.8;
$tx[4]=ball4.translateX=1.3;
$tx[5]=ball5.translateX=-2;
$tx[6]=ball6.translateX=-4.3;
$tx[7]=ball7.translateX=8.8;
$tx[8]=ball8.translateX=16.02;
$tx[9]=ball9.translateX=12.0;
$tx[10]=ball10.translateX=5.2;
$tx[11]=ball1.translateX=-7.9;
$tx[12]=ball2.translateX=13;
$tx[13]=ball3.translateX=-10.8;
$tx[14]=ball4.translateX=21.3;
$tx[15]=ball5.translateX=-12;
$tx[16]=ball6.translateX=-14.3;
$tx[17]=ball7.translateX=28.8;
$tx[18]=ball8.translateX=10.02;
$tx[19]=ball9.translateX=18.0;
$tx[20]=ball10.translateX=15.2; $tz[0]=ball.translateZ;
$tz[1]=ball1.translateZ=1;
$tz[2]=ball2.translateZ=3.347;
$tz[3]=ball3.translateZ=8.908;
$tz[4]=ball4.translateZ=0.736;
$tz[5]=ball5.translateZ=2.525;
$tz[6]=ball6.translateZ=-2.145;
$tz[7]=ball7.translateZ=4.207;
$tz[8]=ball8.translateZ=0.542;
$tz[9]=ball9.translateZ=6.277;
$tz[10]=ball10.translateZ=5;
$tz[11]=ball11.translateZ=-1;
$tz[12]=ball12.translateZ=-3.347;
$tz[13]=ball13.translateZ=-8.908;
$tz[14]=ball14.translateZ=-0.736;
$tz[15]=ball15.translateZ=-2.525;
$tz[16]=ball16.translateZ=-10.145;
$tz[17]=ball17.translateZ=-4.207;
$tz[18]=ball18.translateZ=-5.542;
$tz[19]=ball19.translateZ=16.277;
$tz[20]=ball20.translateZ=15; for($i=1;$i<41;$i=$i 1)
{$aFz[$i]=$afz[$i]=$vz[$i]=$az[$i]=$n[$i]=0;
$z[$i]=$lz[$i]=5;
$aFx[$i]=$afx[$i]=$vx[$i]=$ax[$i]=0;
$lx[$i]=3; } } if(frame>=1)
{
$tz[0]=ball.translateZ;
$tx[0]=50*noise(0.006*frame);
$dz[$k]=$tz[$k]-$tz[0];
$n[$k]=0;
$z[$k]=5;
{for($j=0;$j<41;$j=$j 1) {$dz[$j]=$tz[$j]-$tz[0];
$sign[$k]=sign($vz[$k])*sign($tz[$k]-$tz[$j]);
$dx[$j]=abs($tx[$j]-$tx[$k]);
if((abs($dz[$k]-$dz[$j])<5)
&&($sign[$k]>0)&&($dx[$j]<=5))
{
$lz[$k]=abs($dz[$k]-$dz[$j]);
$lz[$k]=min($lz[$k],$zz[$k]);
$zz[$k]=$lz[$k]; $code[$k]=$j;
$n[$k]=$n[$k] 1; }
}
} }
if($n[$k]==0)
$aFz[$k]=15 0*rand($k) 0*abs($dz[$k]/3);
else
$aFz[$k]=15 0*abs($dz[$k]/3)-$k1*(7-$lz[$k]);
if($tz[$k]<$tz[0])
$aFz[$k]=-$aFz[$k];
if(($lz[$k]<3)&&($n[$k]>0))
$afz[$k]=8*$k2*$vz[$k] 10*sign($vz[$k]);
else
$afz[$k]=$k2*$vz[$k];
$az[$k]=$aFz[$k]-$afz[$k];
if(($lz[$k]<2)&&($n[$k]>0))
$vz[$k]=$vz[$code[$k]];
else
$vz[$k]=$vz[$k] $az[$k]*$t; $tz[$k]=-$vz[$k]*$t-0.5*$az[$k]*$t*$t $tz[$k]; $lx[$k]=$tx[$k]-$tx[$code[$k]];
$dx[$k]=$tx[$k]-$tx[0];
$aFx[$k]=-3*($dx[$k]/5) 0.05*sign($dx[$k]);
if(($lx[$k]<2)&&($n[$k]>0)&&($lz[$k]<2))
{$afx[$k]=-5*sign($lx[$k])*((2.5-$lx[$k])/2)*((2.5-$lx[$k])/2) $k3*$vx[$k];
$ax[$k]=0;}
else if(($n[$k]>0)&&($lz[$k]>=2))
$afx[$k]=-0.1*sign($lx[$k])*((5-$lx[$k])/2) $k3*$vx[$k];
else
$afx[$k]=$k3*$vx[$k];
$ax[$k]=$aFx[$k]-$afx[$k];
$vx[$k]=$vx[$k] $ax[$k]*$t;
$tx[$k]=$tx[$k] $vx[$k]*$t 0.5*$ax[$k]*$t*$t; }
ball.translateX=$tx[0];
ball1.translateX=$tx[1];
ball2.translateX=$tx[2];
ball3.translateX=$tx[3];
ball4.translateX=$tx[4];
ball5.translateX=$tx[5];
ball6.translateX=$tx[6];
ball7.translateX=$tx[7];
ball8.translateX=$tx[8];
ball9.translateX=$tx[9];
ball10.translateX=$tx[10];
ball11.translateX=$tx[11];
ball12.translateX=$tx[12];
ball13.translateX=$tx[13];
ball14.translateX=$tx[14];
ball15.translateX=$tx[15];
ball16.translateX=$tx[16];
ball17.translateX=$tx[17];
ball18.translateX=$tx[18];
ball19.translateX=$tx[19];
ball20.translateX=$tx[20]; ball1.translateZ=$tz[1];
ball2.translateZ=$tz[2];
ball3.translateZ=$tz[3];
ball4.translateZ=$tz[4];
ball5.translateZ=$tz[5];
ball6.translateZ=$tz[6];
ball7.translateZ=$tz[7];
ball8.translateZ=$tz[8];
ball9.translateZ=$tz[9];
ball10.translateZ=$tz[10];
ball11.translateZ=$tz[11];
ball12.translateZ=$tz[12];
ball13.translateZ=$tz[13];
ball14.translateZ=$tz[14];
ball15.translateZ=$tz[15];
ball16.translateZ=$tz[16];
ball17.translateZ=$tz[17];
ball18.translateZ=$tz[18];
ball19.translateZ=$tz[19];
ball20.translateZ=$tz[20]; print("l:" $lx[2] " " $lx[5] " " $lx[10]
" n:" $n[1] ", " $n[2] ", " $n[3] ", " $n[4] ", " $n[5] ", " $n[6] ", " $n[7] ", " $n[8] ", " $n[10] "/n"
" dx:" $dx[2] " " $dx[5] " " $dx[10] "/n"
" aFx:" $aFx[2] " " $aFx[5] " " $aFx[10] "/n"
" ax:" $ax[2] " " $ax[5] " " $ax[10] " " "/n"
" afx:" $afx[2] " " $afx[5] " " $afx[10] "/n"
" vx:" $vx[2] " " $vx[5] " " $vx[10] "/n"
對(duì)于這個(gè)程序僅僅是練習(xí)的東西,還有很多問(wèn)題,例如雖然考慮到了小雞們的穿插情況,但實(shí)際運(yùn)行中依然有可能出現(xiàn)這樣的問(wèn)題。我想應(yīng)該每幀都要對(duì)小雞們重新排序,然后按新的次序關(guān)系計(jì)算相互的影響,前面簡(jiǎn)單的按照初始定義的序號(hào)為次序計(jì)算是不太妥當(dāng)?shù)模袝r(shí)間再改改,還有就是計(jì)算頻率還是太低,現(xiàn)在每幀計(jì)算一次,如果可以每幀計(jì)算多次應(yīng)該會(huì)好很多,由朋友知道如何定義每幀的計(jì)算次數(shù)嗎?當(dāng)然希望有朋友可以提出更好的方法來(lái)。
表達(dá)式可以考慮繼續(xù)完善和擴(kuò)展,例如可以考慮以單個(gè)小雞的奔跑方向來(lái)定義各小雞的局部坐標(biāo),再根據(jù)這個(gè)局部坐標(biāo)來(lái)計(jì)算小計(jì)的奔跑動(dòng)作;可以給各小雞添加不同的屬性,例如可以使每個(gè)小雞的體質(zhì)不同;可以給整個(gè)場(chǎng)景添加圍欄控制,使小雞們?cè)谝欢ǖ姆秶鷥?nèi)奔跑;可以考慮有小雞搶到了小蟲(chóng),小雞們追逐對(duì)象改變的效果;可以考慮用這個(gè)表達(dá)式模擬其他追逐情況或大隊(duì)人馬沖鋒的情景。希望朋友們做出更多更好的效果來(lái)。

