受杰森的《Almost Looks Like Work》啟發,我來展示一些病毒傳播模型。需要注意的是這個模型并不反映現實情況,因此不要誤以為是西非可怕的傳染病。相反,它更應該被看做是某種虛構的僵尸爆發現象。那么,讓我們進入主題。
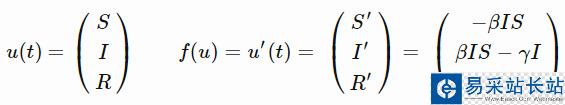
這就是SIR模型,其中字母S、I和R反映的是在僵尸疫情中,個體可能處于的不同狀態。
S 代表易感群體,即健康個體中潛在的可能轉變的數量。 I 代表染病群體,即僵尸數量。 R 代表移除量,即因死亡而退出游戲的僵尸數量,或者感染后又轉回人類的數量。但對與僵尸不存在治愈者,所以我們就不要自我愚弄了(如果要把SIR模型應用到流感傳染中,還是有治愈者的)。 至于β(beta)和γ(gamma): β(beta)表示疾病的傳染性程度,只要被咬就會感染。 γ(gamma)表示從僵尸走向死亡的速率,取決于僵尸獵人的平均工作速率,當然,這不是一個完美的模型,請對我保持耐心。 S′=?βIS告訴我們健康者變成僵尸的速率,S′是對時間的導數。 I′=βIS?γI告訴我們感染者是如何增加的,以及行尸進入移除態速率(雙關語)。 R′=γI只是加上(gamma I),這一項在前面的等式中是負的。上面的模型沒有考慮S/I/R的空間分布,下面來修正一下!
一種方法是把瑞典和北歐國家分割成網格,每個單元可以感染鄰近單元,描述如下:
其中對于單元,和是它周圍的四個單元。(不要因為對角單元而腦疲勞,我們需要我們的大腦不被吃掉)。
初始化一些東東。
import numpy as npimport mathimport matplotlib.pyplot as plt %matplotlib inlinefrom matplotlib import rcParamsimport matplotlib.image as mpimgrcParams['font.family'] = 'serif'rcParams['font.size'] = 16rcParams['figure.figsize'] = 12, 8from PIL import Image
適當的beta和gamma值就能夠摧毀大半江山
beta = 0.010gamma = 1
還記得導數的定義么?當導數已知,假設Δt很小的情況下,經過重新整理,它可以用來近似預測函數的下一個取值,我們已經聲明過u′(t)。
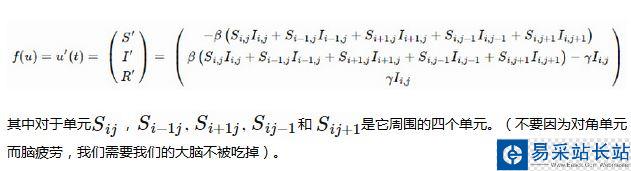
初始化一些東東。
import numpy as npimport mathimport matplotlib.pyplot as plt %matplotlib inlinefrom matplotlib import rcParamsimport matplotlib.image as mpimgrcParams['font.family'] = 'serif'rcParams['font.size'] = 16rcParams['figure.figsize'] = 12, 8from PIL import Image
適當的beta和gamma值就能夠摧毀大半江山
新聞熱點
疑難解答