本文實例講述了Python實現的堆排序算法。分享給大家供大家參考，具體如下：

堆排序的思想: 堆是一種數據結構，可以將堆看作一棵完全二叉樹，這棵二叉樹滿足，任何一個非葉節點的值都不大于（或不小于）其左右孩子節點的值。 將一個無序序列調整為一個堆，就可以找出這個序列的最大值（或最小值），然后將找出的這個值交換到序列的最后一個，這樣有序序列就元素就增加一個，無序序列元素就減少一個，對新的無序序列重復這樣的操作，就實現了排序。

堆排序的執行過程：

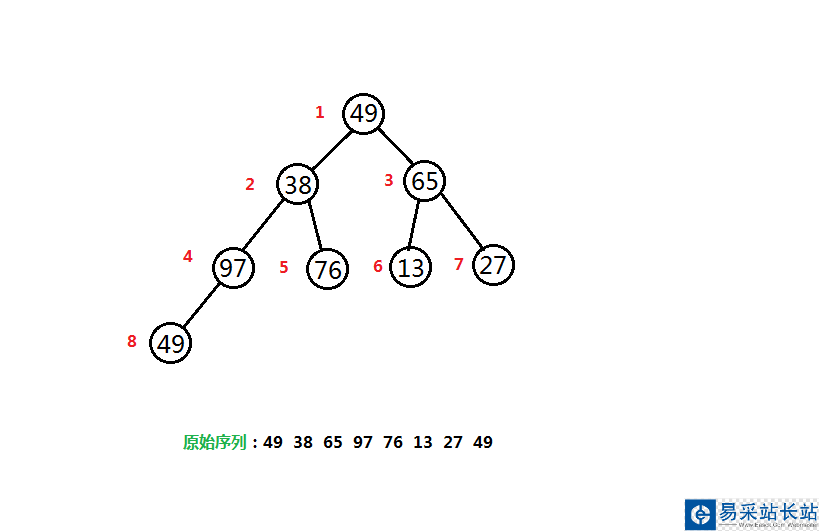
1.從無序序列所確定的完全二叉樹的第一個非葉子節點開始，從右至左，從下至上，對每個節點進行調整，最終將得到一個大頂堆。

對節點的調整方法：將當前節點（假設為a）的值與其孩子節點進行比較，如果存在大于a的值的孩子節點，則從中選出最大的一個與a交換。當a來到下一層的時候重復上述過程，直到a的孩子節點的值都小于a為止

2.將當前無序序列中的第一個元素（反映在數中是根節點b），與無序序列中的最后一個元素交換（假設為c），b進入有序序列，到達最終位置。無序序列元素減少1個，有序序列元素增加1個，此時只有節點c可能不滿足堆的定義，對其進行調整。

3.重復2 的過程，直到無序序列的元素剩下一個時排序結束。

# -*- coding:utf-8 -*-# 堆排序適用于記錄數很多的情況from collections import deque# 這里需要說明元素的存儲必須要從1開始# 涉及到左右節點的定位，和堆排序開始調整節點的定位# 在下標0處插入0，它不參與排序L = deque([49,38,65,97,76,13,27,49])L.appendleft(0)#L = [0,49,38,65,97,76,13,27,49]def element_exchange(numbers,low,high):  temp = numbers[low]  # j 是low的左孩子節點(cheer!)  i = low  j = 2*i  while j<=high:    # 如果右節點較大，則把j指向右節點    if j<high and numbers[j]<numbers[j+1]:      j = j+1    if temp<numbers[j]:      # 將numbers[j]調整到雙親節點的位置上      numbers[i] = numbers[j]      i = j      j = 2*i    else:      break  # 被調整節點放入最終位置  numbers[i] = tempdef top_heap_sort(numbers):  length = len(numbers)-1  # 指定第一個進行調整的元素的下標  # 它即該無序序列完全二叉樹的第一個非葉子節點  # 它之前的元素均要進行調整  # cheer up！  first_exchange_element = length/2  #建立初始堆  print first_exchange_element  for x in range(first_exchange_element):    element_exchange(numbers,first_exchange_element-x,length)  # 將根節點放到最終位置，剩余無序序列繼續堆排序  # length-1 次循環完成堆排序  for y in range(length-1):    temp = numbers[1]    numbers[1] = numbers[length-y]    numbers[length-y] = temp    element_exchange(numbers,1,length-y-1)if __name__=='__main__':  top_heap_sort(L)  for x in range(1,len(L)):    print L[x],