一、分類問題損失函數——交叉熵（crossentropy）

交叉熵刻畫了兩個概率分布之間的距離，是分類問題中使用廣泛的損失函數。給定兩個概率分布p和q，交叉熵刻畫的是兩個概率分布之間的距離：

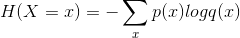
我們可以通過Softmax回歸將神經網絡前向傳播得到的結果變成交叉熵要求的概率分布得分。在TensorFlow中，Softmax回歸的參數被去掉了，只是一個額外的處理層，將神經網絡的輸出變成一個概率分布。

代碼實現：

import tensorflow as tf  y_ = tf.constant([[1.0, 0, 0]]) # 正確標簽 y1 = tf.constant([[0.9, 0.06, 0.04]]) # 預測結果1 y2 = tf.constant([[0.5, 0.3, 0.2]]) # 預測結果2 # 以下為未經過Softmax處理的類別得分 y3 = tf.constant([[10.0, 3.0, 2.0]]) y4 = tf.constant([[5.0, 3.0, 1.0]])  # 自定義交叉熵 cross_entropy1 = -tf.reduce_mean(y_ * tf.log(tf.clip_by_value(y1, 1e-10, 1.0))) cross_entropy2 = -tf.reduce_mean(y_ * tf.log(tf.clip_by_value(y2, 1e-10, 1.0))) # TensorFlow提供的集成交叉熵 # 注：該操作應該施加在未經過Softmax處理的logits上，否則會產生錯誤結果 # labels為期望輸出，且必須采用labels=y_, logits=y的形式將參數傳入 cross_entropy_v2_1 = tf.nn.softmax_cross_entropy_with_logits(labels=y_, logits=y3) cross_entropy_v2_2 = tf.nn.softmax_cross_entropy_with_logits(labels=y_, logits=y4)  sess = tf.InteractiveSession() print('[[0.9, 0.06, 0.04]]:', cross_entropy1.eval()) print('[[0.5, 0.3, 0.2]]:', cross_entropy2.eval()) print('v2_1', cross_entropy_v2_1.eval()) print('v2_2',cross_entropy_v2_2.eval()) sess.close()  ''''' [[0.9, 0.06, 0.04]]: 0.0351202 [[0.5, 0.3, 0.2]]: 0.231049 v2_1 [ 0.00124651] v2_2 [ 0.1429317] ''' 

tf.clip_by_value()函數可將一個tensor的元素數值限制在指定范圍內，這樣可防止一些錯誤運算，起到數值檢查作用。

* 乘法操作符是元素之間直接相乘，tensor中是每個元素對應相乘，要去別去tf.matmul()函數的矩陣相乘。

tf.nn.softmax_cross_entropy_with_logits(labels=y_,logits=y)是TensorFlow提供的集成交叉熵函數。該操作應該施加在未經過Softmax處理的logits上，否則會產生錯誤結果；labels為期望輸出，且必須采用labels=y_, logits=y3的形式將參數傳入。

二、回歸問題損失函數——均方誤差（MSE，mean squared error）

均方誤差亦可用于分類問題的損失函數，其定義為：

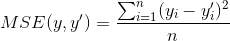
三、自定義損失函數

對于理想的分類問題和回歸問題，可采用交叉熵或者MSE損失函數，但是對于一些實際的問題，理想的損失函數可能在表達上不能完全表達損失情況，以至于影響對結果的優化。例如：對于產品銷量預測問題，表面上是一個回歸問題，可使用MSE損失函數。可實際情況下，當預測值大于實際值時，損失值應是正比于商品成本的函數；當預測值小于實際值，損失值是正比于商品利潤的函數，多數情況下商品成本和利潤是不對等的。自定義損失函數如下：