一、BN（Batch Normalization）算法

1. 對數據進行歸一化處理的重要性

神經網絡學習過程的本質就是學習數據分布，在訓練數據與測試數據分布不同情況下，模型的泛化能力就大大降低；另一方面，若訓練過程中每批batch的數據分布也各不相同，那么網絡每批迭代學習過程也會出現較大波動，使之更難趨于收斂，降低訓練收斂速度。對于深層網絡，網絡前幾層的微小變化都會被網絡累積放大，則訓練數據的分布變化問題會被放大，更加影響訓練速度。

2. BN算法的強大之處

1）為了加速梯度下降算法的訓練，我們可以采取指數衰減學習率等方法在初期快速學習，后期緩慢進入全局最優區域。使用BN算法后，就可以直接選擇比較大的學習率，且設置很大的學習率衰減速度，大大提高訓練速度。即使選擇了較小的學習率，也會比以前不使用BN情況下的收斂速度快。總結就是BN算法具有快速收斂的特性。

2）BN具有提高網絡泛化能力的特性。采用BN算法后，就可以移除針對過擬合問題而設置的dropout和L2正則化項，或者采用更小的L2正則化參數。

3）BN本身是一個歸一化網絡層，則局部響應歸一化層（Local Response Normalization，LRN層）則可不需要了（Alexnet網絡中使用到）。

3. BN算法概述

BN算法提出了變換重構，引入了可學習參數γ、β，這就是算法的關鍵之處：

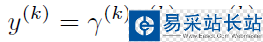
引入這兩個參數后，我們的網絡便可以學習恢復出原是網絡所要學習的特征分布，BN層的錢箱傳到過程如下：

其中m為batchsize。BatchNormalization中所有的操作都是平滑可導，這使得back propagation可以有效運行并學到相應的參數γ，β。需要注意的一點是Batch Normalization在training和testing時行為有所差別。Training時μβ和σβ由當前batch計算得出；在Testing時μβ和σβ應使用Training時保存的均值或類似的經過處理的值，而不是由當前batch計算。

二、TensorFlow相關函數

1.tf.nn.moments(x, axes, shift=None, name=None, keep_dims=False)

x是輸入張量，axes是在哪個維度上求解， 即想要 normalize的維度, [0] 代表 batch 維度，如果是圖像數據，可以傳入 [0, 1, 2]，相當于求[batch, height, width] 的均值/方差，注意不要加入channel 維度。該函數返回兩個張量，均值mean和方差variance。

2.tf.identity(input, name=None)

返回與輸入張量input形狀和內容一致的張量。

3.tf.nn.batch_normalization(x, mean, variance, offset, scale, variance_epsilon,name=None)

計算公式為scale(x - mean)/ variance + offset。

這些參數中，tf.nn.moments可得到均值mean和方差variance，offset和scale是可訓練的，offset一般初始化為0，scale初始化為1，offset和scale的shape與mean相同，variance_epsilon參數設為一個很小的值如0.001。