線性回歸屬于監督學習,因此方法和監督學習應該是一樣的,先給定一個訓練集,根據這個訓練集學習出一個線性函數,然后測試這個函數訓練的好不好(即此函數是否足夠擬合訓練集數據),挑選出最好的函數(cost function最小)即可。
單變量線性回歸:
a) 因為是線性回歸,所以學習到的函數為線性函數,即直線函數;
b) 因為是單變量,因此只有一個x。
我們能夠給出單變量線性回歸的模型:
我們常稱x為feature,h(x)為hypothesis。
上面介紹的方法中,我們肯定有一個疑問,怎樣能夠看出線性函數擬合的好不好呢?
所以此處,我們需要使用到Cost Function(代價函數),代價函數越小,說明線性回歸也越好(和訓練集合擬合的越好),當然最小就是0,即完全擬合。
舉個實際的例子:
我們想要根據房子的大小,預測房子的價格,給定如下數據集:
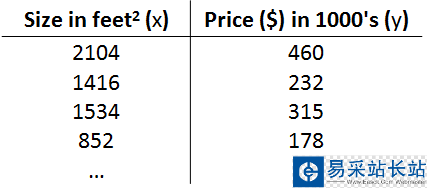
根據上面的數據集,畫出如下所示的圖:
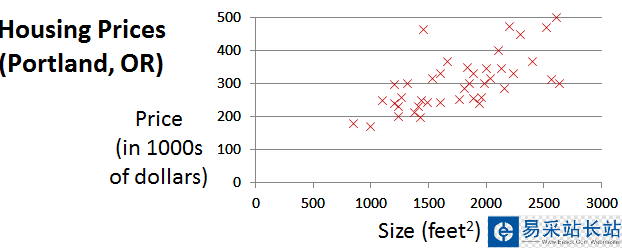
我們需要根據這些點擬合出一條直線,使得Cost Function最小。雖然現在我們還不知道Cost Function內部到底是什么樣的,但是我們的目標是:給定輸入向量x,輸出向量y,theta向量,輸出Cost值。
Cost Function:
Cost Function的用途:對假設的函數進行評價,Cost Function越小的函數,說明對訓練數據擬合的越好。
下圖詳細說明了當Cost Function為黑盒的時候,Cost Function的作用:

但是我們肯定想知道Cost Function的內部結構是什么?因此我們給出下面的公式:
其中:
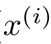 表示向量x中的第i個元素;
表示向量x中的第i個元素;
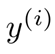 表示向量y中的第i個元素;
表示向量y中的第i個元素;
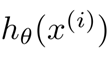 表示已知的假設函數;m表示訓練集的數量。
表示已知的假設函數;m表示訓練集的數量。
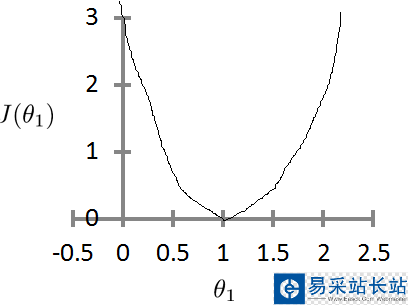
如果theta0一直為0,則theta1與J的函數為:
新聞熱點
疑難解答