本文介紹了python opencv之SURF算法示例，分享給大家，具體如下：

目標：

SURF算法基礎 opencv總SURF算法的使用

原理：

上節課使用了SIFT算法，當時這種算法效率不高，需要更快速的算法。在06年有人提出了SURF算法“加速穩定特征”，從名字上來看，他是SIFT算法的加速版本。

（原文）
在SIFT算法當中使用高斯差分方程（Difference of Gaussian）對高斯拉普拉斯方程( Laplacian of Gaussian）進行近似。然而，SURF使用盒子濾波器進行近似，下面的圖片顯示了這種近似的方法。在進行卷積計算的時候可以利用積分圖像，這是使用盒子形濾波器的一個優點，即計算某個窗口中的像素和的時候，計算量大小，也就是時間復雜度不受到窗口大小的影響。而且，這種運算可以在不用的尺度空間當中實現。

SURF算法計算關鍵點的尺度和位置信息使用Hessian矩陣實現。

（解釋）
文中的高斯拉普拉斯方程（算子）是檢測圖像中斑點的一種十分常用的方法。以一維高斯函數來檢測一維信號中的斑點為例。有一維信號f，高斯函數的一階導數ddxg" role="presentation">ddxg，信號與高斯函數的一階導數卷積后，會在邊緣處出現極值。如圖：

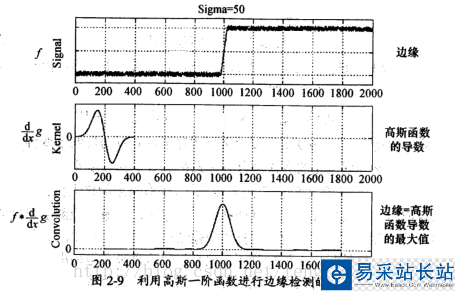
上面圖片是在一維情況下，使用高斯函數的一階導數的情況，另一種方法是使用高斯函數的二階導數與信號進行卷積，高斯函數的二階導數也叫做拉普拉斯變換。

但是，在一維信號斑點檢測的實際情況當中，一個斑點可以考慮成是兩個相鄰的跳突組成，如下圖。

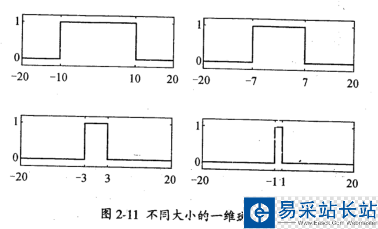
類似于在圖像當中，一個輪胎可以當成一個斑點，一個蒼蠅也可以當成一個斑點。但是在使用高斯函數的二階導數來檢測斑點的時候，使用不同的高斯核（就是方差）運算不同大小的斑點時，計算出來的極值，即響應值會出現衰減。

此時，需要將高斯函數的二階導數進行正規化，去除方差值不同導致響應值出現的衰減。

以上，是一維高斯函數檢測一維信號的原理。二維的圖像信號，使用二維高斯函數來檢測斑點原理基本相同，此處的二維高斯函數的二階導數，就叫做高斯拉普拉斯算子也就是LOG，通過改變不同的方差值，可以檢測不同尺寸的二維斑點，如圖。