本文主要內容：

先上一張gif的k均值聚類算法動態(tài)圖片，讓大家對算法有個感性認識：

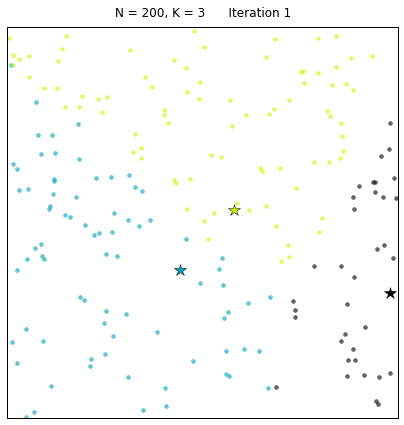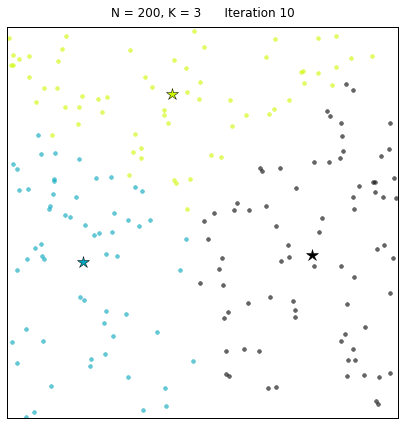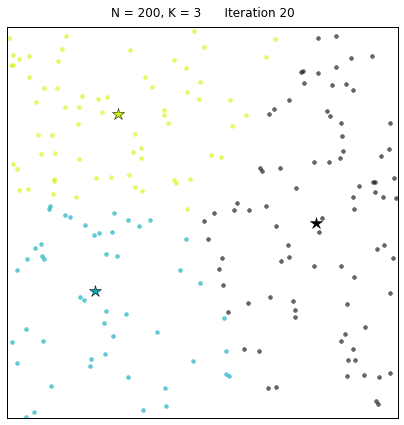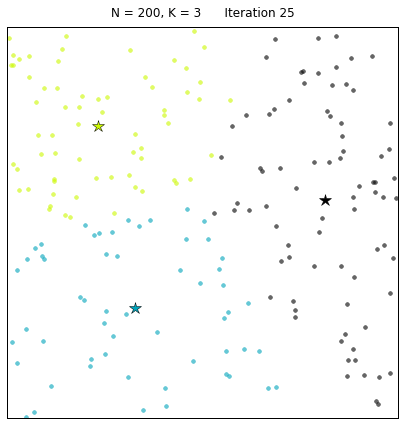
其中：N=200代表有200個樣本，不同的顏色代表不同的簇(其中 3種顏色為3個簇)，星星代表每個簇的簇心。算法通過25次迭代找到收斂的簇心，以及對應的簇。 每次迭代的過程中，簇心和對應的簇都在變化。

聚類算法的特點

聚類算法是無監(jiān)督學習算法和前面的有監(jiān)督算法不同，訓練數據集可以不指定類別(也可以指定)。聚類算法對象歸到同一簇中，類似全自動分類。簇內的對象越相似，聚類的效果越好。K-均值聚類是每個類別簇都是采用簇中所含值的均值計算而成。

聚類樣本間的屬性(包括，有序屬性、無序屬性)度量標準 1. 有序屬性

例如：西瓜的甜度：0.1， 0.5， 0.9(值越大，代表越甜)

我們可以使用明可夫斯基距離定義:

2. 無序屬性

例如：色澤，青綠、淺綠、深綠（又例如: 性別: 男, 女， 中性，人yao…明顯也不能使用0.1， 0.2 等表示求距離）。這些不能使用連續(xù)的值表示，求距離的，一般使用VDM計算：

聚類的常見算法，原型聚類(主要論述K均值聚類)，層次聚類、密度聚類

聚類算法分為如下三大類：

1. 原型聚類(包含3個子類算法)：

K均值聚類算法

學習向量量化

高斯混合聚類

2. 密度聚類：

3. 層次聚類：

下面主要說明K均值聚類算法(示例來源于，周志華西瓜書)

算法基本思想：

K-Means 是發(fā)現給定數據集的 K 個簇的聚類算法, 之所以稱之為 K-均值 是因為它可以發(fā)現 K 個不同的簇,且每個簇的中心采用簇中所含值的均值計算而成.簇個數 K 是用戶指定的, 每一個簇通過其質心（centroid）, 即簇中所有點的中心來描述.

算法流程如下：

主要是三個步驟：