從這節算是開始進入“正規”的機器學習了吧，之所以“正規”因為它開始要建立價值函數（cost function），接著優化價值函數求出權重，然后測試驗證。這整套的流程是機器學習必經環節。今天要學習的話題是邏輯回歸，邏輯回歸也是一種有監督學習方法（supervised machine learning）。邏輯回歸一般用來做預測，也可以用來做分類，預測是某個類別^.^！線性回歸想比大家都不陌生了，y=kx+b,給定一堆數據點，擬合出k和b的值就行了，下次給定X時，就可以計算出y,這就是回歸。而邏輯回歸跟這個有點區別，它是一種非線性函數，擬合功能頗為強大，而且它是連續函數，可以對其求導，這點很重要，如果一個函數不可求導，那它在機器學習用起來很麻煩，早期的海維賽德（Heaviside）階梯函數就因此被sigmoid函數取代，因為可導意味著我們可以很快找到其極值點，這就是優化方法的重要思想之一：利用求導，得到梯度，然后用梯度下降法更新參數。

        下面來看看邏輯回歸的sigmoid函數，如（圖一）所示：

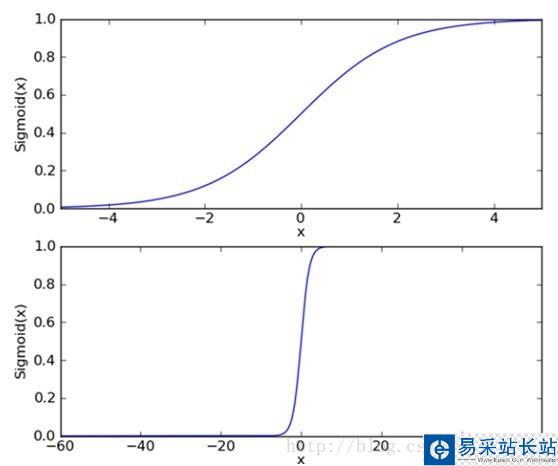
（圖一）

            （圖一）中上圖是sigmoid函數在定義域[-5,5] 上的形狀，而下圖是在定義域[-60,60]上的形狀，由這兩個圖可以看出，它比較適合做二類的回歸，因為嚴重兩級分化。Sigmoid函數的如（公式一）所示：

（公式一）

         現在有了二類回歸函數模型，就可以把特征映射到這個模型上了，而且sigmoid函數的自變量只有一個Z，假設我們的特征為X=[x0,x1,x2…xn]。令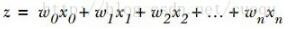，當給定大批的訓練樣本特征X時，我們只要找到合適的W=[w0,w1,w2…wn]來正確的把每個樣本特征X映射到sigmoid函數的兩級上，也就是說正確的完成了類別回歸就行了，那么以后來個測試樣本，只要和權重相乘后，帶入sigmoid函數計算出的值就是預測值啦，很簡單是吧。那怎么求權重W呢？

          要計算W，就要進入優化求解階段咯，用的方法是梯度下降法或者隨機梯度下降法。說到梯度下降，梯度下降一般對什么求梯度呢？梯度是一個函數上升最快的方向，沿著梯度方向我們可以很快找到極值點。我們找什么極值？仔細想想，當然是找訓練模型的誤差極值，當模型預測值和訓練樣本給出的正確值之間的誤差和最小時，模型參數就是我們要求的。當然誤差最小有可能導致過擬合，這個以后再說。我們先建立模型訓練誤差價值函數（cost function），如（公式二）所示：