上節基本完成了SVM的理論推倒，尋找最大化間隔的目標最終轉換成求解拉格朗日乘子變量alpha的求解問題，求出了alpha即可求解出SVM的權重W，有了權重也就有了最大間隔距離，但是其實上節我們有個假設：就是訓練集是線性可分的，這樣求出的alpha在[0,infinite]。但是如果數據不是線性可分的呢？此時我們就要允許部分的樣本可以越過分類器，這樣優化的目標函數就可以不變，只要引入松弛變量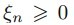即可，它表示錯分類樣本點的代價，分類正確時它等于0，當分類錯誤時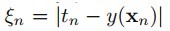，其中Tn表示樣本的真實標簽-1或者1，回顧上節中，我們把支持向量到分類器的距離固定為1，因此兩類的支持向量間的距離肯定大于1的，當分類錯誤時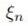肯定也大于1，如（圖五）所示（這里公式和圖標序號都接上一節）。

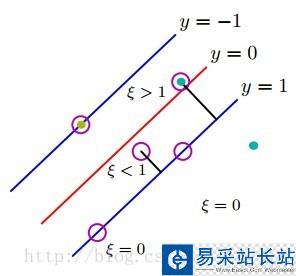
（圖五）

       這樣有了錯分類的代價，我們把上節（公式四）的目標函數上添加上這一項錯分類代價，得到如（公式八）的形式：

（公式八）

重復上節的拉格朗日乘子法步驟，得到（公式九）：

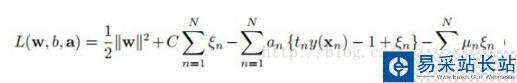
（公式九）

         多了一個Un乘子，當然我們的工作就是繼續求解此目標函數，繼續重復上節的步驟，求導得到（公式十）：

（公式十）

         又因為alpha大于0，而且Un大于0，所以0<alpha<C,為了解釋的清晰一些，我們把（公式九）的KKT條件也發出來（上節中的第三類優化問題），注意Un是大于等于0：

      推導到現在，優化函數的形式基本沒變，只是多了一項錯分類的價值，但是多了一個條件，0<alpha<C，C是一個常數，它的作用就是在允許有錯誤分類的情況下，控制最大化間距，它太大了會導致過擬合，太小了會導致欠擬合。接下來的步驟貌似大家都應該知道了，多了一個C常量的限制條件，然后繼續用SMO算法優化求解二次規劃，但是我想繼續把核函數也一次說了，如果樣本線性不可分，引入核函數后，把樣本映射到高維空間就可以線性可分，如（圖六）所示的線性不可分的樣本：