SVM（support vector machine）支持向量機：

注意：本文不準備提到數學證明的過程，一是因為有一篇非常好的文章解釋的非常好：支持向量機通俗導論（理解SVM的三層境界） ，另一方面是因為我只是個程序員，不是搞數學的（主要是因為數學不好。），主要目的是將SVM以最通俗易懂，簡單粗暴的方式解釋清楚。

線性分類：

先從線性可分的數據講起，如果需要分類的數據都是線性可分的，那么只需要一根直線f(x)=wx+b就可以分開了，類似這樣：

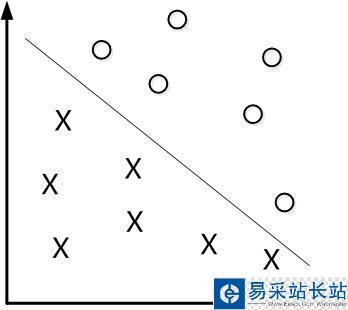
這種方法被稱為：線性分類器，一個線性分類器的學習目標便是要在n維的數據空間中找到一個超平面（hyper plane）。也就是說，數據不總是二維的，比如，三維的超平面是面。但是有個問題：

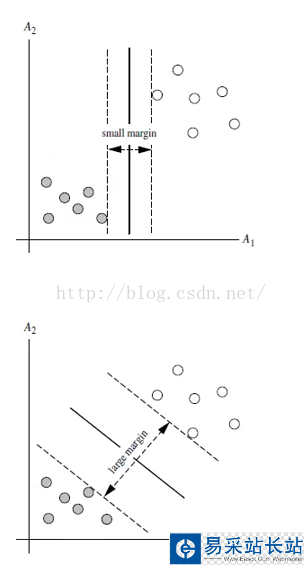
上述兩種超平面，都可以將數據進行分類，由此可推出，其實能有無數個超平面能將數據劃分，但是哪條最優呢？

最大間隔分類器Maximum Margin Classifier：

簡稱MMH， 對一個數據點進行分類，當超平面離數據點的“間隔”越大，分類的確信度（confidence）也越大。所以，為了使得分類的確信度盡量高，需要讓所選擇的超平面能夠最大化這個“間隔”值。這個間隔就是下圖中的Gap的一半。

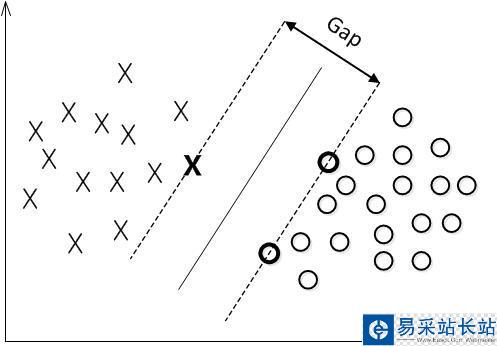
用以生成支持向量的點，如上圖XO，被稱為支持向量點，因此SVM有一個優點，就是即使有大量的數據，但是支持向量點是固定的，因此即使再次訓練大量數據，這個超平面也可能不會變化。

非線性分類：

數據大多數情況都不可能是線性的，那如何分割非線性數據呢？

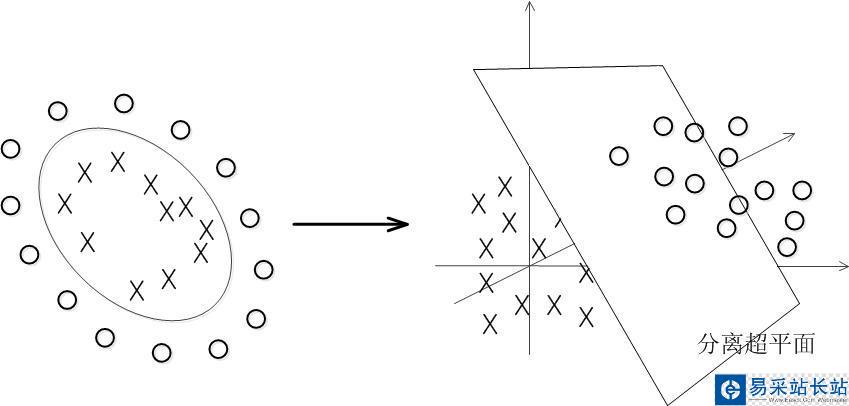
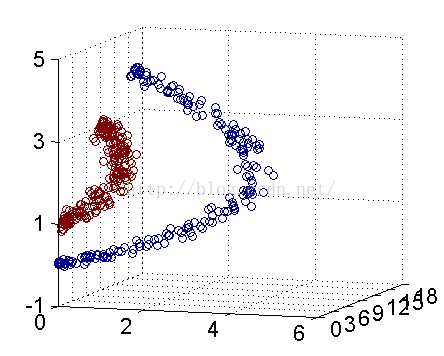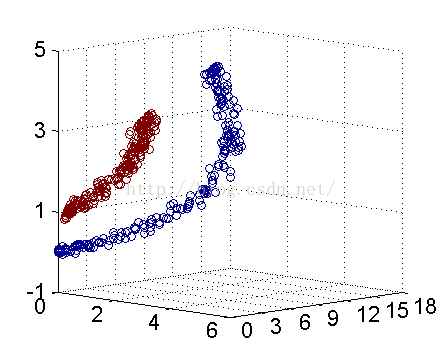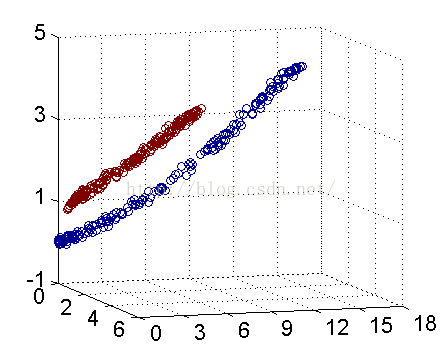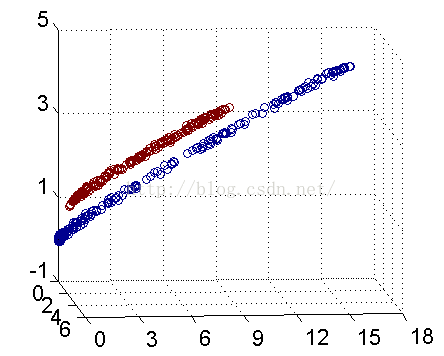
解決方法是將數據放到高維度上再進行分割，如下圖：

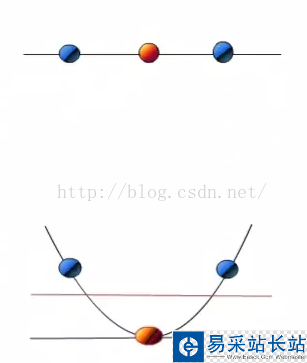
當f(x)=x時，這組數據是個直線，如上半部分，但是當我把這組數據變為f(x)=x^2時，這組數據就變成了下半部分的樣子，也就可以被紅線所分割。

比如說，我這里有一組三維的數據X=（x1,x2,x3），線性不可分割，因此我需要將他轉換到六維空間去。因此我們可以假設六個維度分別是：x1,x2,x3,x1^2,x1*x2,x1*x3，當然還能繼續展開，但是六維的話這樣就足夠了。

新的決策超平面：d(Z)=WZ+b，解出W和b后帶入方程，因此這組數據的超平面應該是：d(Z)=w1x1+w2x2+w3x3+w4*x1^2+w5x1x2+w6x1x3+b但是又有個新問題，轉換高緯度一般是以內積（dot product）的方式進行的，但是內積的算法復雜度非常大。