什么是機器學習 （Machine Learning）

      機器學習是研究計算機怎樣模擬或實現人類的學習行為，以獲取新的知識或技能，重新組織已有的知識結構使之不斷改善自身的性能。它是人工智能的核心，是使計算機具有智能的根本途徑，其應用遍及人工智能的各個領域。

機器學習的大致分類：

1）分類（模式識別）：要求系統依據已知的分類知識對輸入的未知模式（該模式的描述）作分析，以確定輸入模式的類屬，例如手寫識別（識別是不是這個數）。

2）問題求解：要求對于給定的目標狀態,尋找一個將當前狀態轉換為目標狀態的動作序列。

SVM一般是用來分類的（一般先分為兩類，再向多類推廣一生二，二生三，三生萬物哈）

問題的描述

向量表示:假設一個樣本有n個變量(特征)：Ⅹ= (X1,X2,…,Xn)T

樣本表示方法：

SVM線性分類器

SVM從線性可分情況下的最優分類面發展而來。最優分類面就是要求分類線不但能將兩類正確分開(訓練錯誤率為0),且使分類間隔最大。SVM考慮尋找一個滿足分類要求的超平面,并且使訓練集中的點距離分類面盡可能的遠,也就是尋找一個分類面使它兩側的空白區域(margin)最大。

過兩類樣本中離分類面最近的點且平行于最優分類面的超平面上H1,H2的訓練樣本就叫做支持向量。

圖例：

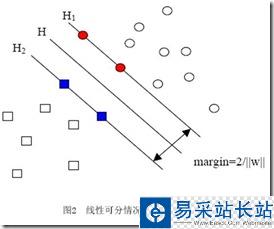
問題描述：

假定訓練數據 ：

可以被分為一個超平面：

進行歸一化：

此時分類間隔等于：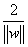

即使得：最大間隔最大等價于使最小

下面這兩張圖可以看一下，有個感性的認識。那個好？

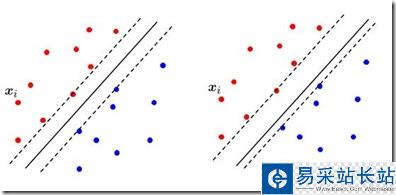
看下面這張圖：

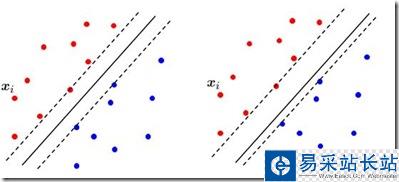
       下面我們要開始優化上面的式子，因為推導要用到拉格朗日定理和KKT條件，所以我們先了解一下相關知識。在求取有約束條件的優化問題時，拉格朗日乘子法（Lagrange Multiplier) 和KKT條件是非常重要的兩個求取方法，對于等式約束的優化問題，可以應用拉格朗日乘子法去求取最優值；如果含有不等式約束，可以應用KKT條件去求取。當然，這兩個方法求得的結果只是必要條件，只有當是凸函數的情況下，才能保證是充分必要條件。KKT條件是拉格朗日乘子法的泛化。之前學習的時候，只知道直接應用兩個方法，但是卻不知道為什么拉格朗日乘子法（Lagrange Multiplier) 和KKT條件能夠起作用，為什么要這樣去求取最優值呢？