從這一章開始進入正式的算法學習。

首先我們學習經典而有效的分類算法：決策樹分類算法。

1、決策樹算法

決策樹用樹形結構對樣本的屬性進行分類，是最直觀的分類算法，而且也可以用于回歸。不過對于一些特殊的邏輯分類會有困難。典型的如異或（XOR）邏輯，決策樹并不擅長解決此類問題。
決策樹的構建不是唯一的，遺憾的是最優(yōu)決策樹的構建屬于NP問題。因此如何構建一棵好的決策樹是研究的重點。
J. Ross Quinlan在1975提出將信息熵的概念引入決策樹的構建，這就是鼎鼎大名的ID3算法。后續(xù)的C4.5, C5.0, CART等都是該方法的改進。

熵就是“無序，混亂”的程度。剛接觸這個概念可能會有些迷惑。想快速了解如何用信息熵增益劃分屬性，可以參考這位兄弟的文章：Python機器學習之決策樹算法

如果還不理解，請看下面這個例子。

假設要構建這么一個自動選好蘋果的決策樹，簡單起見，我只讓他學習下面這4個樣本：
樣本    紅     大      好蘋果 
0         1        1         1 
1         1        0         1 
2         0        1         0 
3         0        0         0 

樣本中有2個屬性，A0表示是否紅蘋果。A1表示是否大蘋果。

那么這個樣本在分類前的信息熵就是S = -(1/2 * log(1/2) + 1/2 * log(1/2)) = 1。

信息熵為1表示當前處于最混亂，最無序的狀態(tài)。

本例僅2個屬性。那么很自然一共就只可能有2棵決策樹，如下圖所示：

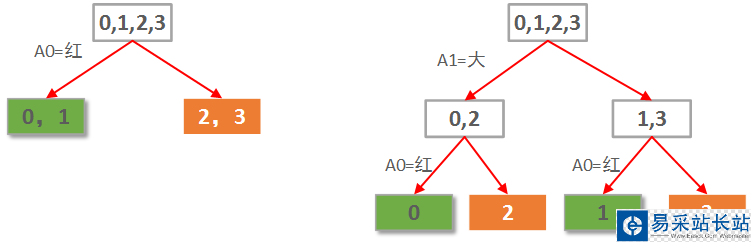
顯然左邊先使用A0（紅色）做劃分依據的決策樹要優(yōu)于右邊用A1（大小）做劃分依據的決策樹。
當然這是直覺的認知。定量的考察，則需要計算每種劃分情況的信息熵增益。
先選A0作劃分，各子節(jié)點信息熵計算如下：
0，1葉子節(jié)點有2個正例，0個負例。信息熵為：e1 = -(2/2 * log(2/2) + 0/2 * log(0/2)) = 0。
2，3葉子節(jié)點有0個正例，2個負例。信息熵為：e2 = -(0/2 * log(0/2) + 2/2 * log(2/2)) = 0。

因此選擇A0劃分后的信息熵為每個子節(jié)點的信息熵所占比重的加權和：E = e1*2/4 + e2*2/4 = 0。
選擇A0做劃分的信息熵增益G（S, A0）=S - E = 1 - 0 = 1.