本文實例為大家分享了Python KNN分類算法的具體代碼，供大家參考，具體內容如下

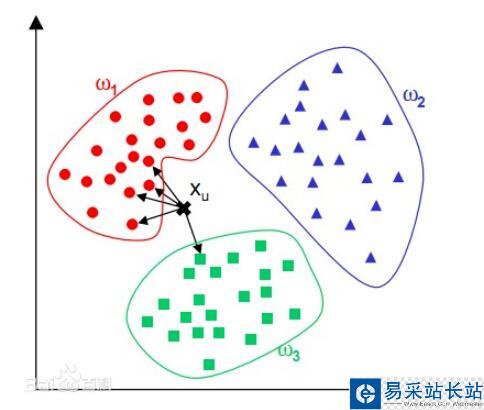
KNN分類算法應該算得上是機器學習中最簡單的分類算法了，所謂KNN即為K-NearestNeighbor（K個最鄰近樣本節點）。在進行分類之前KNN分類器會讀取較多數量帶有分類標簽的樣本數據作為分類的參照數據，當它對類別未知的樣本進行分類時，會計算當前樣本與所有參照樣本的差異大小；該差異大小是通過數據點在樣本特征的多維度空間中的距離來進行衡量的，也就是說，如果兩個樣本點在在其特征數據多維度空間中的距離越近，則這兩個樣本點之間的差異就越小，這兩個樣本點屬于同一類別的可能性就越大。KNN分類算法利用這一基本的認知，通過計算待預測樣本點與參照樣本空間中所有的樣本的距離，并找到K個距離該樣本點最近的參照樣本點，統計出這最鄰近的K個樣本點中占比數量最多的類別，并將該類別作為預測結果。

KNN的模型十分簡單，沒有涉及到模型的訓練，每一次預測都需要計算該點與所有已知點的距離，因此隨著參照樣本集的數量增加，KNN分類器的計算開銷也會呈比例增加，并且KNN并不適合數量很少的樣本集。并且KNN提出之后，后續很多人提出了很多改進的算法，分別從提高算法速率和提高算法準確率兩個方向，但是都是基于“距離越近，相似的可能性越大”的原則。這里利用Python實現了KNN最原始版本的算法，數據集使用的是機器學習課程中使用得非常多的鶯尾花數據集，同時我在原數據集的基礎上向數據集中添加了少量的噪聲數據，測試KNN算法的魯棒性。

數據集用得是鶯尾花數據集，下載地址。

數據集包含90個數據（訓練集），分為2類，每類45個數據，每個數據4個屬性 

Sepal.Length（花萼長度），單位是cm;
Sepal.Width（花萼寬度），單位是cm;
Petal.Length（花瓣長度），單位是cm;
Petal.Width（花瓣寬度），單位是cm;

分類種類： Iris Setosa（山鳶尾）、Iris Versicolour（雜色鳶尾）
之前主打C++，近來才學的Python，今天想拿實現KNN來練練手，下面上代碼：

#coding=utf-8import math#定義鳶尾花的數據類class Iris: data=[] label=[] pass#定義一個讀取鶯尾花數據集的函數def load_dataset(filename="Iris_train.txt"): f=open(filename) line=f.readline().strip() propty=line.split(',')#屬性名 dataset=[]#保存每一個樣本的數據信息 label=[]#保存樣本的標簽 while line: line=f.readline().strip() if(not line): break temp=line.split(',') content=[] for i in temp[0:-1]: content.append(float(i)) dataset.append(content) label.append(temp[-1]) total=Iris() total.data=dataset total.label=label return total#返回數據集 #定義一個Knn分類器類class KnnClassifier: def __init__(self,k,type="Euler"):#初始化的時候定義正整數K和距離計算方式 self.k=k self.type=type self.dataloaded=False def load_traindata(self,traindata):#加載數據集 self.data=traindata.data self.label=traindata.label self.label_set=set(traindata.label) self.dataloaded=True#是否加載數據集的標記  def Euler_dist(self,x,y):# 歐拉距離計算方法，x、y都是向量 sum=0 for i,j in zip(x,y): sum+=math.sqrt((i-j)**2) return sum def Manhattan_dist(self,x,y):#曼哈頓距離計算方法，x、y都是向量 sum=0 for i,j in zip(x,y): sum+=abs(i-j) return sum def predict(self,temp):#預測函數，讀入一個預測樣本的數據，temp是一個向量 if(not self.dataloaded):#判斷是否有訓練數據 print "No train_data load in" return distance_and_label=[] if(self.type=="Euler"):#判斷距離計算方式，歐拉距離或者曼哈頓距離 for i,j in zip(self.data,self.label): dist=self.Euler_dist(temp,i) distance_and_label.append([dist,j]) else: if(self.type=="Manhattan"): for i,j in zip(self.data,self.label): dist=self.Manhattan_dist(temp,i) distance_and_label.append([dist,j]) else: print "type choice error" #獲取K個最鄰近的樣本的距離和類別標簽 neighborhood=sorted(distance_and_label,cmp=lambda x,y : cmp(x[0],y[0]))[0:self.k] neighborhood_class=[] for i in neighborhood: neighborhood_class.append(i[1]) class_set=set(neighborhood_class) neighborhood_class_count=[] print "In k nearest neighborhoods:" #統計該K個最鄰近點中各個類別的個數 for i in class_set: a=neighborhood_class.count(i) neighborhood_class_count.append([i,a]) print "class: ",i," count: ",a result=sorted(neighborhood_class_count,cmp=lambda x,y : cmp(x[1],y[1]))[-1][0] print "result: ",result return result#返回預測的類別 if __name__ == '__main__': traindata=load_dataset()#training data testdata=load_dataset("Iris_test.txt")#testing data #新建一個Knn分類器的K為20，默認為歐拉距離計算方式 kc=KnnClassifier(20) kc.load_traindata(traindata) predict_result=[] #預測測試集testdata中所有待預測樣本的結果 for i,j in zip(testdata.data,testdata.label): predict_result.append([i,kc.predict(i),j]) correct_count=0 #將預測結果和正確結果進行比對，計算該次預測的準確率 for i in predict_result: if(i[1]==i[2]): correct_count+=1 ratio=float(correct_count)/len(predict_result) print "correct predicting ratio",ratio