機器學習中的預(yù)測問題通常分為2類:回歸與分類。
簡單的說回歸就是預(yù)測數(shù)值,而分類是給數(shù)據(jù)打上標簽歸類。
本文講述如何用Python進行基本的數(shù)據(jù)擬合,以及如何對擬合結(jié)果的誤差進行分析。
本例中使用一個2次函數(shù)加上隨機的擾動來生成500個點,然后嘗試用1、2、100次方的多項式對該數(shù)據(jù)進行擬合。
擬合的目的是使得根據(jù)訓練數(shù)據(jù)能夠擬合出一個多項式函數(shù),這個函數(shù)能夠很好的擬合現(xiàn)有數(shù)據(jù),并且能對未知的數(shù)據(jù)進行預(yù)測。
代碼如下:
import matplotlib.pyplot as plt import numpy as np import scipy as sp from scipy.stats import norm from sklearn.pipeline import Pipeline from sklearn.linear_model import LinearRegression from sklearn.preprocessing import PolynomialFeatures from sklearn import linear_model ''''' 數(shù)據(jù)生成 ''' x = np.arange(0, 1, 0.002) y = norm.rvs(0, size=500, scale=0.1) y = y + x**2 ''''' 均方誤差根 ''' def rmse(y_test, y): return sp.sqrt(sp.mean((y_test - y) ** 2)) ''''' 與均值相比的優(yōu)秀程度,介于[0~1]。0表示不如均值。1表示完美預(yù)測.這個版本的實現(xiàn)是參考scikit-learn官網(wǎng)文檔 ''' def R2(y_test, y_true): return 1 - ((y_test - y_true)**2).sum() / ((y_true - y_true.mean())**2).sum() ''''' 這是Conway&White《機器學習使用案例解析》里的版本 ''' def R22(y_test, y_true): y_mean = np.array(y_true) y_mean[:] = y_mean.mean() return 1 - rmse(y_test, y_true) / rmse(y_mean, y_true) plt.scatter(x, y, s=5) degree = [1,2,100] y_test = [] y_test = np.array(y_test) for d in degree: clf = Pipeline([('poly', PolynomialFeatures(degree=d)), ('linear', LinearRegression(fit_intercept=False))]) clf.fit(x[:, np.newaxis], y) y_test = clf.predict(x[:, np.newaxis]) print(clf.named_steps['linear'].coef_) print('rmse=%.2f, R2=%.2f, R22=%.2f, clf.score=%.2f' % (rmse(y_test, y), R2(y_test, y), R22(y_test, y), clf.score(x[:, np.newaxis], y))) plt.plot(x, y_test, linewidth=2) plt.grid() plt.legend(['1','2','100'], loc='upper left') plt.show() 該程序運行的顯示結(jié)果如下:
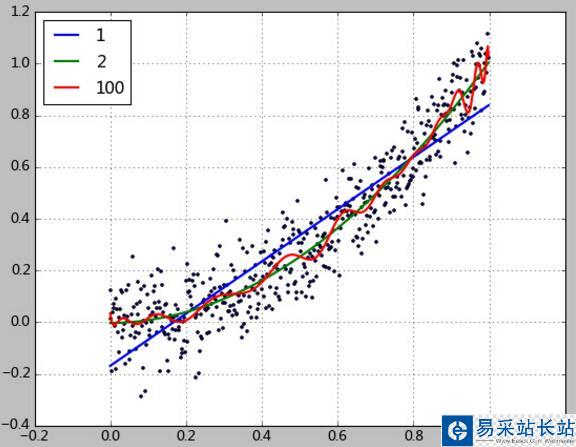
[-0.16140183 0.99268453]
rmse=0.13, R2=0.82, R22=0.58, clf.score=0.82
[ 0.00934527 -0.03591245 1.03065829]
rmse=0.11, R2=0.88, R22=0.66, clf.score=0.88
[ 6.07130354e-02 -1.02247150e+00 6.66972089e+01 -1.85696012e+04
......
-9.43408707e+12 -9.78954604e+12 -9.99872105e+12 -1.00742526e+13
-1.00303296e+13 -9.88198843e+12 -9.64452002e+12 -9.33298267e+12
-1.00580760e+12]
rmse=0.10, R2=0.89, R22=0.67, clf.score=0.89
顯示出的coef_就是多項式參數(shù)。如1次擬合的結(jié)果為
y = 0.99268453x -0.16140183
新聞熱點
疑難解答