決策樹分類與上一篇博客k近鄰分類的最大的區別就在于，k近鄰是沒有訓練過程的，而決策樹是通過對訓練數據進行分析，從而構造決策樹，通過決策樹來對測試數據進行分類，同樣是屬于監督學習的范疇。決策樹的結果類似如下圖：

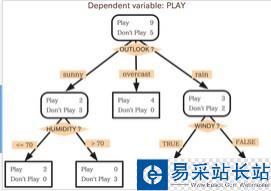
圖中方形方框代表葉節點，帶圓邊的方框代表決策節點，決策節點與葉節點的不同之處就是決策節點還需要通過判斷該節點的狀態來進一步分類。

那么如何通過訓練數據來得到這樣的決策樹呢？

這里涉及要信息論中一個很重要的信息度量方式，香農熵。通過香農熵可以計算信息增益。

香農熵的計算公式如下：

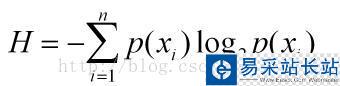
p(xi)代表數據被分在i類的概率，可以通過計算數據集中i類的個數與總的數據個數之比得到，計算香農熵的python代碼如下：

from math import log def calcShannonEnt(dataSet):   numEntries=len(dataSet)   labelCounts={}   for featVec in dataSet:     currentLabel=featVec[-1]     if currentLabel not in labelCounts.keys():       labelCounts[currentLabel]=0     labelCounts[currentLabel]+=1   shannonEnt=0.0   for key in labelCounts:     prob=float(labelCounts[key])/numEntries     shannonEnt-=prob*log(prob,2)   return shannonEnt 

一般來說，數據集中，不同的類別越多，即信息量越大，那么熵值越大，通過計算熵，就可以知道選擇哪一個特征能夠最好的分開數據，這個特征就是一個決策節點。

下面就可以根據訓練數據開始構造決策樹。

首先編寫一個根據給定特征劃分數據集的函數：

#劃分數據集，返回第axis軸為value值的數據集 def splitDataSet(dataset,axis,value):   retDataSet=[]   for featVec in dataset:     if featVec[axis]==value:       reducedFeatVec=featVec[:]       del(reducedFeatVec[axis])       retDataSet.append(reducedFeatVec)   return retDataSet 

下面找出數據集中能夠最好劃分數據的那個特征，它的原理是計算經過每一個特征軸劃分后的數據的信息增益，信息增益越大，代表通過該特征軸劃分是最優的。

#選擇最好的數據集劃分方式，返回最佳的軸 def chooseBestFeatureToSplit(dataset):   numFeatures=len(dataset[0])-1   baseEntrypy=calcShannonEnt(dataset)   bestInfoGain=0.0   bestFeature=-1   for i in range(numFeatures):     featList=[example[i] for example in dataset]     uniqueVals=set(featList)     newEntrypy=0.0     for value in uniqueVals:       subDataSet=splitDataSet(dataset,i,value)       prob=len(subDataSet)/float(len(dataset))       newEntrypy+=prob*calcShannonEnt(subDataSet)     infoGain=baseEntrypy-newEntrypy        #計算信息增益，信息增益最大，就是最好的劃分     if infoGain>bestInfoGain:       bestInfoGain=infoGain       bestFeature=i   return bestFeature