想當初，考研的時候要是知道有這么個好東西，計算定積分。。。開玩笑，那時候計算定積分根本沒有這么簡單的。但這確實給我打開了一種思路，用編程語言去解決更多更復雜的數學問題。下面進入正題。

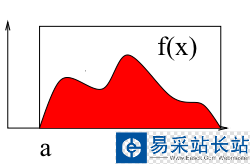
如上圖所示，計算區間[a b]上f(x)的積分即求曲線與X軸圍成紅色區域的面積。下面使用蒙特卡洛法計算區間[2 3]上的定積分：∫(x2+4*x*sin(x))dx

# -*- coding: utf-8 -*-import numpy as npimport matplotlib.pyplot as pltdef f(x):  return x**2 + 4*x*np.sin(x) def intf(x):   return x**3/3.0+4.0*np.sin(x) - 4.0*x*np.cos(x)a = 2;  b = 3; # use N draws N= 10000X = np.random.uniform(low=a, high=b, size=N) # N values uniformly drawn from a to b Y =f(X)  # CALCULATE THE f(x) # 蒙特卡洛法計算定積分：面積=寬度*平均高度Imc= (b-a) * np.sum(Y)/ N;exactval=intf(b)-intf(a)print "Monte Carlo estimation=",Imc, "Exact number=", intf(b)-intf(a)# --How does the accuracy depends on the number of points(samples)? Lets try the same 1-D integral # The Monte Carlo methods yield approximate answers whose accuracy depends on the number of draws.Imc=np.zeros(1000)Na = np.linspace(0,1000,1000)exactval= intf(b)-intf(a)for N in np.arange(0,1000):  X = np.random.uniform(low=a, high=b, size=N) # N values uniformly drawn from a to b   Y =f(X)  # CALCULATE THE f(x)   Imc[N]= (b-a) * np.sum(Y)/ N;   plt.plot(Na[10:],np.sqrt((Imc[10:]-exactval)**2), alpha=0.7)plt.plot(Na[10:], 1/np.sqrt(Na[10:]), 'r')plt.xlabel("N")plt.ylabel("sqrt((Imc-ExactValue)$^2$)")plt.show()

>>>

Monte Carlo estimation= 11.8181144118 Exact number= 11.8113589251

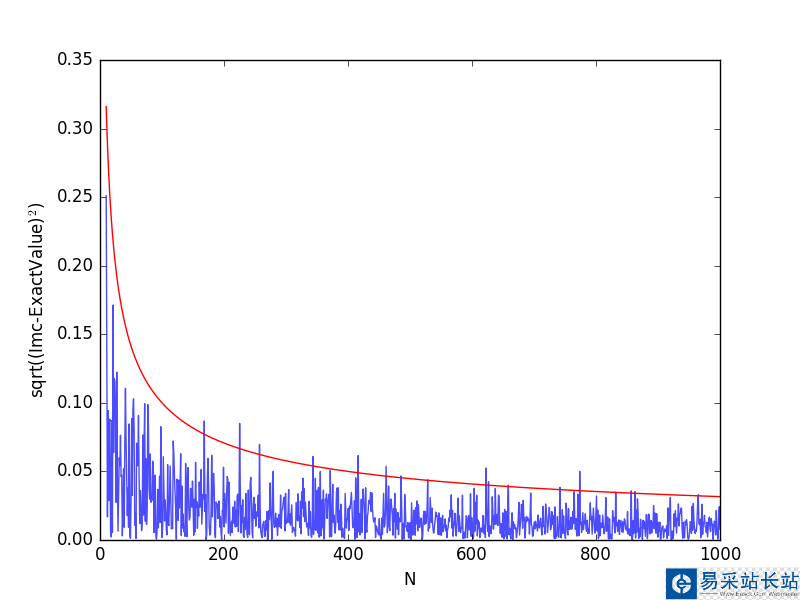
從上圖可以看出，隨著采樣點數的增加，計算誤差逐漸減小。想要提高模擬結果的精確度有兩個途徑：其一是增加試驗次數N；其二是降低方差σ2. 增加試驗次數勢必使解題所用計算機的總時間增加，要想以此來達到提高精度之目的顯然是不合適的。下面來介紹重要抽樣法來減小方差，提高積分計算的精度。

重要性抽樣法的特點在于，它不是從給定的過程的概率分布抽樣，而是從修改的概率分布抽樣，使對模擬結果有重要作用的事件更多出現，從而提高抽樣效率，減少花費在對模擬結果無關緊要的事件上的計算時間。比如在區間[a b]上求g(x)的積分，若采用均勻抽樣，在函數值g(x)比較小的區間內產生的抽樣點跟函數值較大處區間內產生的抽樣點的數目接近，顯然抽樣效率不高，可以將抽樣概率密度函數改為f(x)，使f(x)與g(x)的形狀相近，就可以保證對積分計算貢獻較大的抽樣值出現的機會大于貢獻小的抽樣值，即可以將積分運算改寫為：