本文實(shí)例講述了Java分治歸并排序算法。分享給大家供大家參考，具體如下：

1、分治法

許多有用的算法在結(jié)構(gòu)上是遞歸的：為了解決一個(gè)給定的問(wèn)題，算法一次或多次遞歸地調(diào)用其自身以解決緊密相關(guān)的若干子問(wèn)題。這些算法典型地遵循分治法的思想：將原問(wèn)題分解為幾個(gè)規(guī)模較小但類似于原問(wèn)題的子問(wèn)題，遞歸地求解這些子問(wèn)題，然后再合并這些子問(wèn)題的解來(lái)建立原問(wèn)題的解。

分治模式在每層遞歸時(shí)都有三個(gè)步驟：

（1）分解原問(wèn)題為若干子問(wèn)題，這些子問(wèn)題是原問(wèn)題的規(guī)模較小的實(shí)例。
（2）解決這些子問(wèn)題，遞歸地求解各子問(wèn)題。然而，若子問(wèn)題的規(guī)模足夠小，則直接求解。
（3）合并這些子問(wèn)題的解成原問(wèn)題的解。

2、歸并排序算法

歸并排序算法完全遵循分治模式。直觀上其操作如下：

（1）分解：分解待排序的n個(gè)元素的序列成各具n/2個(gè)元素的兩個(gè)子序列。
（2）解決：使用歸并排序遞歸地排序兩個(gè)子序列。
（3）合并：合并兩個(gè)已排序的子序列以產(chǎn)生已排序的答案。

當(dāng)待排序的序列長(zhǎng)度為1時(shí)，遞歸“開(kāi)始回升”，在這種情況下不要做任何工作，因?yàn)殚L(zhǎng)度為1的每個(gè)序列都已排好序。歸并排序算法的關(guān)鍵操作是“合并”步驟中兩個(gè)已排序序列的合并。我們通過(guò)調(diào)用一個(gè)輔助過(guò)程Merge(A,p,q,r)來(lái)完成合并，其中A是一個(gè)數(shù)組，p、q和r是數(shù)組下標(biāo)，滿足p<=q<r。該過(guò)程假設(shè)子數(shù)組A[p,q]和A[q+1,r]都已排好序。它合并這兩個(gè)子數(shù)組形成單一的已排好序的子數(shù)組并代替當(dāng)前的子數(shù)組A[p,r]。

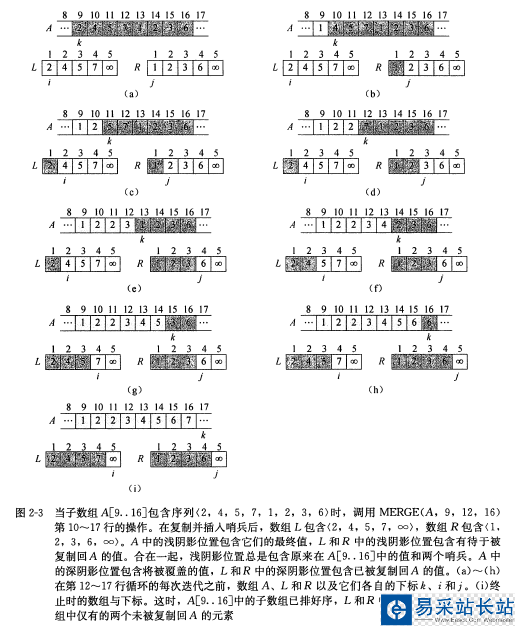
過(guò)程Merge按以下方式工作。回到我們玩撲克牌的例子，假設(shè)桌上有兩堆牌面朝上的牌，每堆都已排序，最小的牌在頂上。我們希望把這兩堆牌合并成單一的排好序的輸出堆，牌面朝下地放在桌上。我們的基本步驟包括在牌面朝上的兩堆牌的頂上兩張牌中選取較小的一張，將該牌從其堆中移開(kāi)（該堆的頂上將顯露一張新牌）并牌面朝下地將該牌放置到輸出堆。

下面是Merge的偽代碼：

Merge(A,p,q,r)：

tmp[1,..,r-p+1]i = pj = q+1while i <= q && j <= r  if A[i] <= A[j]  tmp[k++] = A[i++];  else  tmp[k++] = A[j++];  while i <= q  tmp[k++] = A[i++];  while j <= r  tmp[k++] = A[j++];  for k2 = 0 to tmp.length  A[k2+p] = tmp[k2];

現(xiàn)在我們可以把過(guò)程Merge作為歸并排序算法中的一個(gè)子程序來(lái)用。下面的過(guò)程Merge_sort(A,p,r)排序子數(shù)組A[p,r]中的元素。若p>=r，則該子數(shù)組最多有一個(gè)元素，所以已經(jīng)排好序。否則，分解步驟簡(jiǎn)單地計(jì)算一個(gè)下標(biāo)q，將A[p,r]分成兩個(gè)子數(shù)組A[p,q]和A[q+1,r]，前者包含[n/2]個(gè)元素，后者包含[n/2]個(gè)元素。