本文實例講述了Python機器學習之決策樹算法。分享給大家供大家參考，具體如下：

決策樹學習是應用最廣泛的歸納推理算法之一，是一種逼近離散值目標函數的方法，在這種方法中學習到的函數被表示為一棵決策樹。決策樹可以使用不熟悉的數據集合，并從中提取出一系列規則，機器學習算法最終將使用這些從數據集中創造的規則。決策樹的優點為：計算復雜度不高，輸出結果易于理解，對中間值的缺失不敏感，可以處理不相關特征數據。缺點為：可能產生過度匹配的問題。決策樹適于處理離散型和連續型的數據。

在決策樹中最重要的就是如何選取用于劃分的特征

在算法中一般選用ID3，D3算法的核心問題是選取在樹的每個節點要測試的特征或者屬性，希望選擇的是最有助于分類實例的屬性。如何定量地衡量一個屬性的價值呢？這里需要引入熵和信息增益的概念。熵是信息論中廣泛使用的一個度量標準，刻畫了任意樣本集的純度。

假設有10個訓練樣本，其中6個的分類標簽為yes，4個的分類標簽為no，那熵是多少呢？在該例子中，分類的數目為2（yes，no），yes的概率為0.6，no的概率為0.4，則熵為 ：

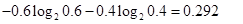
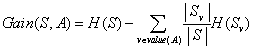
其中value（A）是屬性A所有可能值的集合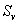，是S中屬性A的值為v的子集，即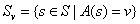。上述公式的第一項為原集合S的熵，第二項是用A分類S后熵的期望值，該項描述的期望熵就是每個子集的熵的加權和，權值為屬于的樣本占原始樣本S的比例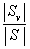。所以Gain(S, A)是由于知道屬性A的值而導致的期望熵減少。

完整的代碼：

# -*- coding: cp936 -*-from numpy import *import operatorfrom math import logimport operatordef createDataSet():  dataSet = [[1,1,'yes'],    [1,1,'yes'],    [1,0,'no'],    [0,1,'no'],    [0,1,'no']]  labels = ['no surfacing','flippers']  return dataSet, labelsdef calcShannonEnt(dataSet):  numEntries = len(dataSet)  labelCounts = {} # a dictionary for feature  for featVec in dataSet:    currentLabel = featVec[-1]    if currentLabel not in labelCounts.keys():      labelCounts[currentLabel] = 0    labelCounts[currentLabel] += 1  shannonEnt = 0.0  for key in labelCounts:    #print(key)    #print(labelCounts[key])    prob = float(labelCounts[key])/numEntries    #print(prob)    shannonEnt -= prob * log(prob,2)  return shannonEnt#按照給定的特征劃分數據集#根據axis等于value的特征將數據提出def splitDataSet(dataSet, axis, value):  retDataSet = []  for featVec in dataSet:    if featVec[axis] == value:      reducedFeatVec = featVec[:axis]      reducedFeatVec.extend(featVec[axis+1:])      retDataSet.append(reducedFeatVec)  return retDataSet#選取特征，劃分數據集，計算得出最好的劃分數據集的特征def chooseBestFeatureToSplit(dataSet):  numFeatures = len(dataSet[0]) - 1 #剩下的是特征的個數  baseEntropy = calcShannonEnt(dataSet)#計算數據集的熵，放到baseEntropy中  bestInfoGain = 0.0;bestFeature = -1 #初始化熵增益  for i in range(numFeatures):    featList = [example[i] for example in dataSet] #featList存儲對應特征所有可能得取值    uniqueVals = set(featList)    newEntropy = 0.0    for value in uniqueVals:#下面是計算每種劃分方式的信息熵,特征i個，每個特征value個值      subDataSet = splitDataSet(dataSet, i ,value)      prob = len(subDataSet)/float(len(dataSet)) #特征樣本在總樣本中的權重      newEntropy = prob * calcShannonEnt(subDataSet)    infoGain = baseEntropy - newEntropy #計算i個特征的信息熵    #print(i)    #print(infoGain)    if(infoGain > bestInfoGain):      bestInfoGain = infoGain      bestFeature = i  return bestFeature#如上面是決策樹所有的功能模塊#得到原始數據集之后基于最好的屬性值進行劃分，每一次劃分之后傳遞到樹分支的下一個節點#遞歸結束的條件是程序遍歷完成所有的數據集屬性，或者是每一個分支下的所有實例都具有相同的分類#如果所有實例具有相同的分類，則得到一個葉子節點或者終止快#如果所有屬性都已經被處理，但是類標簽依然不是確定的，那么采用多數投票的方式#返回出現次數最多的分類名稱def majorityCnt(classList):  classCount = {}  for vote in classList:    if vote not in classCount.keys():classCount[vote] = 0    classCount[vote] += 1  sortedClassCount = sorted(classCount.iteritems(),key=operator.itemgetter(1), reverse=True)  return sortedClassCount[0][0]#創建決策樹def createTree(dataSet,labels):  classList = [example[-1] for example in dataSet]#將最后一行的數據放到classList中，所有的類別的值  if classList.count(classList[0]) == len(classList): #類別完全相同不需要再劃分    return classList[0]  if len(dataSet[0]) == 1:#這里為什么是1呢？就是說特征數為1的時候    return majorityCnt(classList)#就返回這個特征就行了，因為就這一個特征  bestFeat = chooseBestFeatureToSplit(dataSet)  print('the bestFeatue in creating is :')  print(bestFeat)  bestFeatLabel = labels[bestFeat]#運行結果'no surfacing'  myTree = {bestFeatLabel:{}}#嵌套字典,目前value是一個空字典  del(labels[bestFeat])  featValues = [example[bestFeat] for example in dataSet]#第0個特征對應的取值  uniqueVals = set(featValues)  for value in uniqueVals: #根據當前特征值的取值進行下一級的劃分    subLabels = labels[:]    myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet,bestFeat,value),subLabels)  return myTree#對上面簡單的數據進行小測試def testTree1():  myDat,labels=createDataSet()  val = calcShannonEnt(myDat)  print 'The classify accuracy is: %.2f%%' % val  retDataSet1 = splitDataSet(myDat,0,1)  print (myDat)  print(retDataSet1)  retDataSet0 = splitDataSet(myDat,0,0)  print (myDat)  print(retDataSet0)  bestfeature = chooseBestFeatureToSplit(myDat)  print('the bestFeatue is :')  print(bestfeature)  tree = createTree(myDat,labels)  print(tree)