Python說(shuō)來(lái)簡(jiǎn)單也簡(jiǎn)單，但是也不簡(jiǎn)單，尤其是再跟高數(shù)結(jié)合起來(lái)的時(shí)候。。。

正態(tài)分布（Normaldistribution），也稱“常態(tài)分布”，又名高斯分布（Gaussiandistribution），最早由A.棣莫弗在求二項(xiàng)分布的漸近公式中得到。C.F.高斯在研究測(cè)量誤差時(shí)從另一個(gè)角度導(dǎo)出了它。P.S.拉普拉斯和高斯研究了它的性質(zhì)。是一個(gè)在數(shù)學(xué)、物理及工程等領(lǐng)域都非常重要的概率分布，在統(tǒng)計(jì)學(xué)的許多方面有著重大的影響力。

正態(tài)曲線呈鐘型，兩頭低，中間高，左右對(duì)稱因其曲線呈鐘形，因此人們又經(jīng)常稱之為鐘形曲線。

若隨機(jī)變量X服從一個(gè)數(shù)學(xué)期望為μ、方差為σ^2的正態(tài)分布，記為

N(μ，σ^2)

其概率密度函數(shù)為正態(tài)分布的期望值μ決定了其位置，其標(biāo)準(zhǔn)差σ決定了分布的幅度。當(dāng)μ=0,σ=1時(shí)的正態(tài)分布是標(biāo)準(zhǔn)正態(tài)分布。其概率密度函數(shù)為：

我們通常所說(shuō)的標(biāo)準(zhǔn)正態(tài)分布是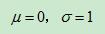的正態(tài)分布：

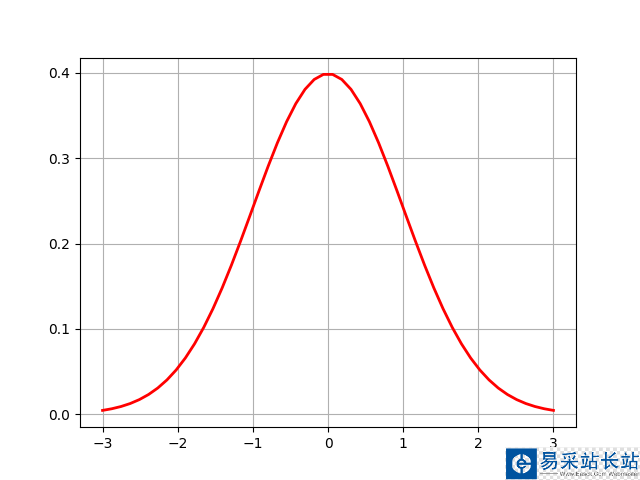
概率密度函數(shù)

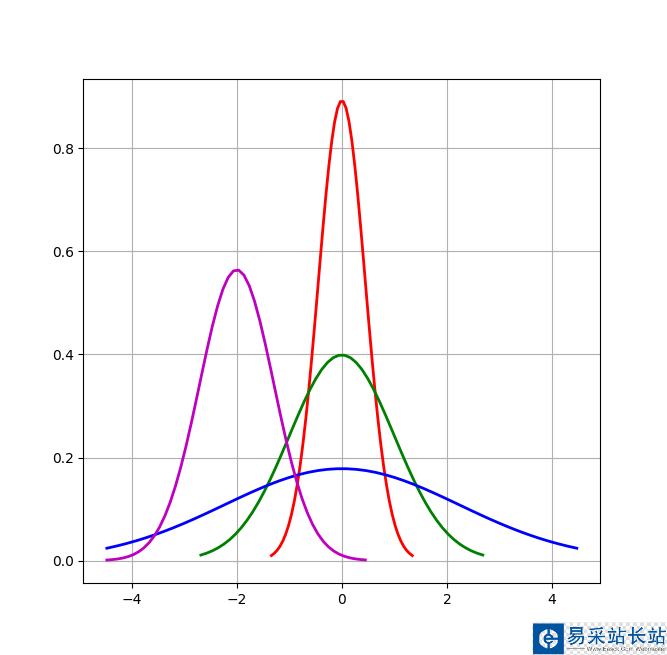
代碼實(shí)現(xiàn)：

 # Python實(shí)現(xiàn)正態(tài)分布 # 繪制正態(tài)分布概率密度函數(shù) u = 0 # 均值μ u01 = -2 sig = math.sqrt(0.2) # 標(biāo)準(zhǔn)差δ sig01 = math.sqrt(1) sig02 = math.sqrt(5) sig_u01 = math.sqrt(0.5) x = np.linspace(u - 3*sig, u + 3*sig, 50) x_01 = np.linspace(u - 6 * sig, u + 6 * sig, 50) x_02 = np.linspace(u - 10 * sig, u + 10 * sig, 50) x_u01 = np.linspace(u - 10 * sig, u + 1 * sig, 50) y_sig = np.exp(-(x - u) ** 2 /(2* sig **2))/(math.sqrt(2*math.pi)*sig) y_sig01 = np.exp(-(x_01 - u) ** 2 /(2* sig01 **2))/(math.sqrt(2*math.pi)*sig01) y_sig02 = np.exp(-(x_02 - u) ** 2 / (2 * sig02 ** 2)) / (math.sqrt(2 * math.pi) * sig02) y_sig_u01 = np.exp(-(x_u01 - u01) ** 2 / (2 * sig_u01 ** 2)) / (math.sqrt(2 * math.pi) * sig_u01) plt.plot(x, y_sig, "r-", linewidth=2) plt.plot(x_01, y_sig01, "g-", linewidth=2) plt.plot(x_02, y_sig02, "b-", linewidth=2) plt.plot(x_u01, y_sig_u01, "m-", linewidth=2) # plt.plot(x, y, 'r-', x, y, 'go', linewidth=2,markersize=8) plt.grid(True) plt.show()

總結(jié)

以上就是本文關(guān)于Python數(shù)據(jù)可視化正態(tài)分布簡(jiǎn)單分析及實(shí)現(xiàn)代碼的全部?jī)?nèi)容，希望對(duì)大家有所幫助。感興趣的朋友可以繼續(xù)參閱本站其他Python和算法相關(guān)專題，如有不足之處，歡迎留言指出。感謝朋友們對(duì)本站的支持！