求一個(gè)數(shù)的平方根函數(shù)sqrt(int num) ,在大多數(shù)語(yǔ)言中都提供實(shí)現(xiàn)。那么要求一個(gè)數(shù)的平方根,是怎么實(shí)現(xiàn)的呢?
實(shí)際上求平方根的算法方法主要有兩種:二分法(binary search)和牛頓迭代法(Newton iteration)
1:二分法
求根號(hào)5
a:折半: 5/2=2.5
b:平方校驗(yàn): 2.5*2.5=6.25>5,并且得到當(dāng)前上限2.5
c:再次向下折半:2.5/2=1.25
d:平方校驗(yàn):1.25*1.25=1.5625<5,得到當(dāng)前下限1.25
e:再次折半:2.5-(2.5-1.25)/2=1.875
f:平方校驗(yàn):1.875*1.875=3.515625<5,得到當(dāng)前下限1.875
每次得到當(dāng)前值和5進(jìn)行比較,并且記下下下限和上限,依次迭代,逐漸逼近平方根:
import math from math import sqrt def sqrt_binary(num): x=sqrt(num) y=num/2.0 low=0.0 up=num*1.0 count=1 while abs(y-x)>0.00000001: print count,y count+=1 if (y*y>num): up=y y=low+(y-low)/2 else: low=y y=up-(up-y)/2 return y print(sqrt_binary(5)) print(sqrt(5))
運(yùn)行結(jié)果:
1 2.5
2 1.25
3 1.875
4 2.1875
5 2.34375
6 2.265625
7 2.2265625
8 2.24609375
9 2.236328125
10 2.2314453125
11 2.23388671875
12 2.23510742188
13 2.23571777344
14 2.23602294922
15 2.23617553711
16 2.23609924316
17 2.23606109619
18 2.23608016968
19 2.23607063293
20 2.23606586456
21 2.23606824875
22 2.23606705666
23 2.2360676527
24 2.23606795073
25 2.23606809974
26 2.23606802523
27 2.23606798798
2.23606796935
2.2360679775
[Finished in 0.1s]
經(jīng)過(guò)27次二分法迭代,得到的值和系統(tǒng)sqrt()差別在0.00000001,精度在億分之一,
0.001需要迭代8次
因此,在對(duì)精度要求不高的情況下,二分法也算比較高效的算法。
2:牛頓迭代
仔細(xì)思考一下就能發(fā)現(xiàn),我們需要解決的問(wèn)題可以簡(jiǎn)單化理解。
從函數(shù)意義上理解:我們是要求函數(shù)f(x)=x²,使f(x)=num的近似解,即x²-num=0的近似解。
從幾何意義上理解:我們是要求拋物線g(x)=x²-num與x軸交點(diǎn)(g(x)=0)最接近的點(diǎn)。
我們假設(shè)g(x0)=0,即x0是正解,那么我們要做的就是讓近似解x不斷逼近x0,這是函數(shù)導(dǎo)數(shù)的定義:
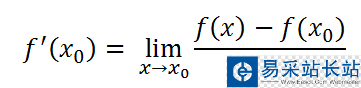
可以由此得到
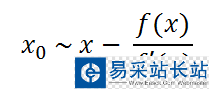
從幾何圖形上看,因?yàn)閷?dǎo)數(shù)是切線,通過(guò)不斷迭代,導(dǎo)數(shù)與x軸的交點(diǎn)會(huì)不斷逼近x0。
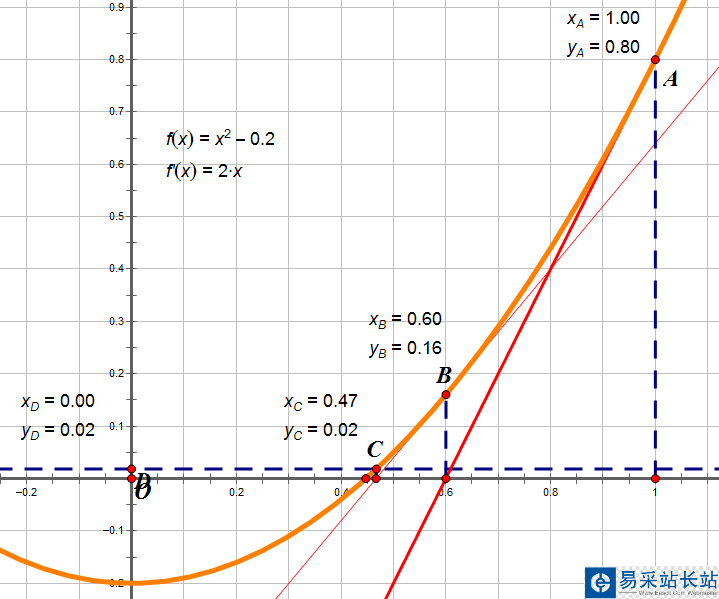
對(duì)于一般情況:
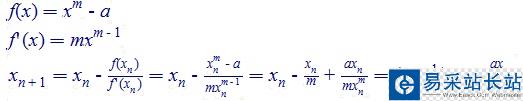
新聞熱點(diǎn)
疑難解答
圖片精選