概率論啊概率論，差不多忘完了。

基于概率論的分類方法：樸素貝葉斯

1. 概述

貝葉斯分類是一類分類算法的總稱，這類算法均以貝葉斯定理為基礎(chǔ)，故統(tǒng)稱為貝葉斯分類。本章首先介紹貝葉斯分類算法的基礎(chǔ)——貝葉斯定理。最后，我們通過實例來討論貝葉斯分類的中最簡單的一種: 樸素貝葉斯分類。

2. 貝葉斯理論 & 條件概率

2.1 貝葉斯理論

我們現(xiàn)在有一個數(shù)據(jù)集，它由兩類數(shù)據(jù)組成，數(shù)據(jù)分布如下圖所示：

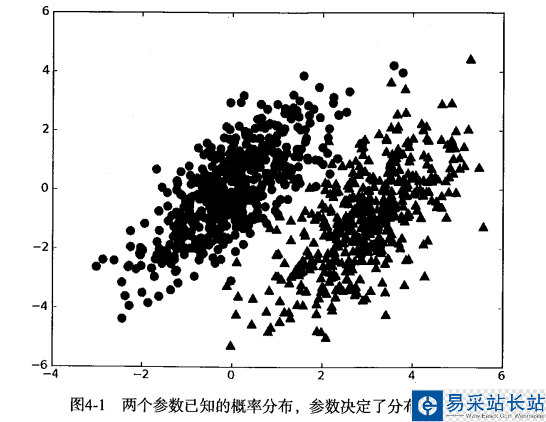
我們現(xiàn)在用 p1(x,y) 表示數(shù)據(jù)點 (x,y) 屬于類別 1（圖中用圓點表示的類別）的概率，用 p2(x,y) 表示數(shù)據(jù)點 (x,y) 屬于類別 2（圖中三角形表示的類別）的概率，那么對于一個新數(shù)據(jù)點 (x,y)，可以用下面的規(guī)則來判斷它的類別：

如果 p1(x,y) > p2(x,y) ，那么類別為1如果 p2(x,y) > p1(x,y) ，那么類別為2

也就是說，我們會選擇高概率對應(yīng)的類別。這就是貝葉斯決策理論的核心思想，即選擇具有最高概率的決策。

2.1.2 條件概率

如果你對 p(x,y|c1) 符號很熟悉，那么可以跳過本小節(jié)。

有一個裝了 7 塊石頭的罐子，其中 3 塊是白色的，4 塊是黑色的。如果從罐子中隨機取出一塊石頭，那么是白色石頭的可能性是多少？由于取石頭有 7 種可能，其中 3 種為白色，所以取出白色石頭的概率為 3/7 。那么取到黑色石頭的概率又是多少呢？很顯然，是 4/7 。我們使用 P(white) 來表示取到白色石頭的概率，其概率值可以通過白色石頭數(shù)目除以總的石頭數(shù)目來得到。

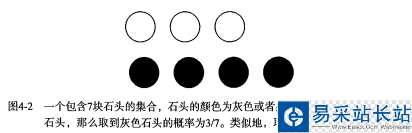
如果這 7 塊石頭如下圖所示，放在兩個桶中，那么上述概率應(yīng)該如何計算？

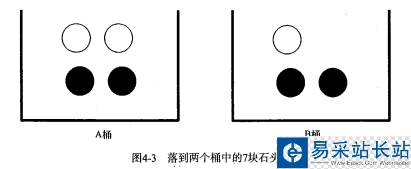
計算 P(white) 或者 P(black) ，如果事先我們知道石頭所在桶的信息是會改變結(jié)果的。這就是所謂的條件概率（conditional probablity）。假定計算的是從 B 桶取到白色石頭的概率，這個概率可以記作 P(white|bucketB) ，我們稱之為“在已知石頭出自 B 桶的條件下，取出白色石頭的概率”。很容易得到，P(white|bucketA) 值為 2/4 ，P(white|bucketB) 的值為 1/3 。

條件概率的計算公式如下：

P(white|bucketB) = P(white and bucketB) / P(bucketB)

首先，我們用 B 桶中白色石頭的個數(shù)除以兩個桶中總的石頭數(shù)，得到 P(white and bucketB) = 1/7 .其次，由于 B 桶中有 3 塊石頭，而總石頭數(shù)為 7 ，于是 P(bucketB) 就等于 3/7 。于是又 P(white|bucketB) = P(white and bucketB) / P(bucketB) = (1/7) / (3/7) = 1/3 。

另外一種有效計算條件概率的方法稱為貝葉斯準則。貝葉斯準則告訴我們?nèi)绾谓粨Q條件概率中的條件與結(jié)果，即如果已知 P(x|c)，要求 P(c|x)，那么可以使用下面的計算方法：