決策樹原理：從數據集中找出決定性的特征對數據集進行迭代劃分，直到某個分支下的數據都屬于同一類型，或者已經遍歷了所有劃分數據集的特征，停止決策樹算法。

　　每次劃分數據集的特征都有很多，那么我們怎么來選擇到底根據哪一個特征劃分數據集呢？這里我們需要引入信息增益和信息熵的概念。

一、信息增益

　　劃分數據集的原則是：將無序的數據變的有序。在劃分數據集之前之后信息發生的變化稱為信息增益。知道如何計算信息增益，我們就可以計算根據每個特征劃分數據集獲得的信息增益，選擇信息增益最高的特征就是最好的選擇。首先我們先來明確一下信息的定義：符號xi的信息定義為 l(xi)=-log2 p(xi)，p(xi)為選擇該類的概率。那么信息源的熵H=-∑p(xi)·log2 p(xi)。根據這個公式我們下面編寫代碼計算香農熵

def calcShannonEnt(dataSet): NumEntries = len(dataSet) labelsCount = {} for i in dataSet:  currentlabel = i[-1]  if currentlabel not in labelsCount.keys():   labelsCount[currentlabel]=0  labelsCount[currentlabel]+=1 ShannonEnt = 0.0 for key in labelsCount:  prob = labelsCount[key]/NumEntries  ShannonEnt -= prob*log(prob,2) return ShannonEnt

上面的自定義函數我們需要在之前導入log方法，from math import log。 我們可以先用一個簡單的例子來測試一下

def createdataSet(): #dataSet = [['1','1','yes'],['1','0','no'],['0','1','no'],['0','0','no']] dataSet = [[1,1,'yes'],[1,0,'no'],[0,1,'no'],[0,0,'no']] labels = ['no surfacing','flippers'] return dataSet,labels

這里的熵為0.811，當我們增加數據的類別時，熵會增加。這里更改后的數據集的類別有三種‘yes'、‘no'、‘maybe'，也就是說數據越混亂，熵就越大。

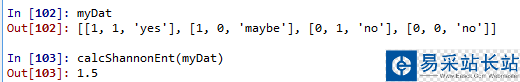
分類算法出了需要計算信息熵，還需要劃分數據集。決策樹算法中我們對根據每個特征劃分的數據集計算一次熵，然后判斷按照哪個特征劃分是最好的劃分方式。

def splitDataSet(dataSet,axis,value): retDataSet = [] for featVec in dataSet:  if featVec[axis] == value:   reducedfeatVec = featVec[:axis]   reducedfeatVec.extend(featVec[axis+1:])   retDataSet.append(reducedfeatVec) return retDataSet

axis表示劃分數據集的特征，value表示特征的返回值。這里需要注意extend方法和append方法的區別。舉例來說明這個區別

下面我們測試一下劃分數據集函數的結果：

axis=0，value=1，按myDat數據集的第0個特征向量是否等于1進行劃分。