本文接上一篇博客python實現的八大排序算法part1,將繼續使用python實現八大排序算法中的剩余四個:快速排序、堆排序、歸并排序、基數排序
5、快速排序
快速排序是通常被認為在同數量級(O(nlog2n))的排序方法中平均性能最好的。
算法思想:
已知一組無序數據a[1]、a[2]、……a[n],需將其按升序排列。首先任取數據a[x]作為基準。比較a[x]與其它數據并排序,使a[x]排在數據的第k位,并且使a[1]~a[k-1]中的每一個數據<a[x],a[k+1]~a[n]中的每一個數據>a[x],然后采用分治的策略分別對a[1]~a[k-1]和a[k+1]~a[n]兩組數據進行快速排序。
優點:極快,數據移動少;
缺點:不穩定。
python代碼實現:
def quick_sort(list): little = [] pivotList = [] large = [] # 遞歸出口 if len(list) <= 1: return list else: # 將第一個值做為基準 pivot = list[0] for i in list: # 將比基準小的值放到less數列 if i < pivot: little.append(i) # 將比基準大的值放到more數列 elif i > pivot: large.append(i) # 將和基準相同的值保存在基準數列 else: pivotList.append(i) # 對less數列和more數列繼續進行快速排序 little = quick_sort(little) large = quick_sort(large) return little + pivotList + large
下面這段代碼出自《Python cookbook 第二版的三行實現python快速排序。
#!/usr/bin/env python#coding:utf-8'''file:python-8sort.pydate:9/1/17 9:03 AMauthor:lockeyemail:lockey@123.comdesc:python實現八大排序算法'''lst = [65,568,9,23,4,34,65,8,6,9]def quick_sort(list): if len(list) <= 1: return list else: pivot = list[0] return quick_sort([x for x in list[1:] if x < pivot]) + / [pivot] + / quick_sort([x for x in list[1:] if x >= pivot])
運行測試結果截圖:
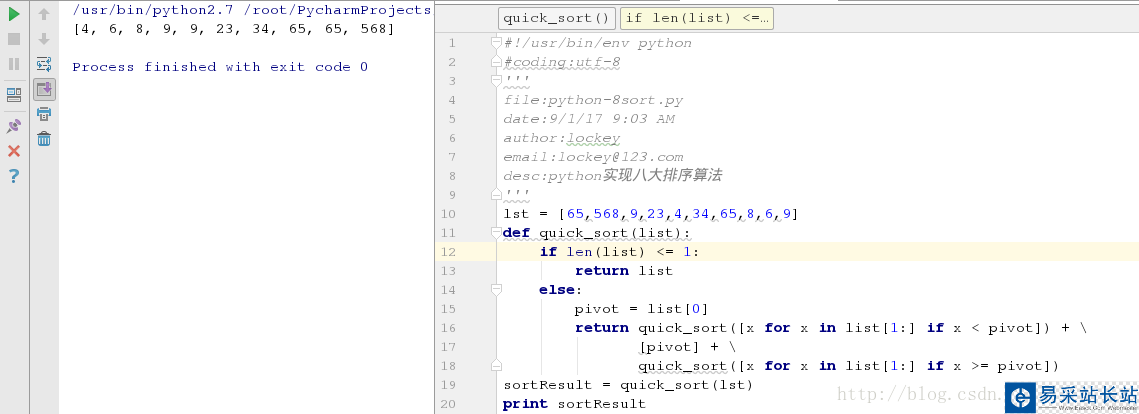
好吧,還有更精簡的語法糖,一行完事:
quick_sort = lambda xs : ( (len(xs) <= 1 and [xs]) or [ quick_sort( [x for x in xs[1:] if x < xs[0]] ) + [xs[0]] + quick_sort( [x for x in xs[1:] if x >= xs[0]] ) ] )[0]
若初始序列按關鍵碼有序或基本有序時,快排序反而蛻化為冒泡排序。為改進之,通常以“三者取中法”來選取基準記錄,即將排序區間的兩個端點與中點三個記錄關鍵碼居中的調整為支點記錄。快速排序是一個不穩定的排序方法。
在改進算法中,我們將只對長度大于k的子序列遞歸調用快速排序,讓原序列基本有序,然后再對整個基本有序序列用插入排序算法排序。實踐證明,改進后的算法時間復雜度有所降低,且當k取值為 8 左右時,改進算法的性能最佳。
新聞熱點
疑難解答