本文主要給大家介紹了梯度下降法及利用Python實現的相關內容，分享出來供大家參考學習，下面話不多說，來一起看看詳細的介紹吧。

梯度下降法介紹

梯度下降法（gradient descent），又名最速下降法（steepest descent）是求解無約束最優化問題最常用的方法，它是一種迭代方法，每一步主要的操作是求解目標函數的梯度向量，將當前位置的負梯度方向作為搜索方向（因為在該方向上目標函數下降最快，這也是最速下降法名稱的由來）。

梯度下降法特點：越接近目標值，步長越小，下降速度越慢。

直觀上來看如下圖所示：

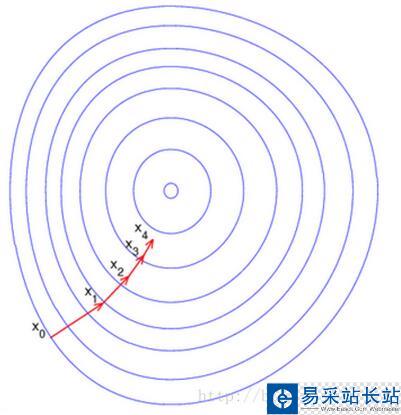
這里每一個圈代表一個函數梯度，最中心表示函數極值點，每次迭代根據當前位置求得的梯度（用于確定搜索方向以及與步長共同決定前進速度）和步長找到一個新的位置，這樣不斷迭代最終到達目標函數局部最優點（如果目標函數是凸函數，則到達全局最優點）。

下面我們將通過公式來具體說明梯度下降法

下面這個h(θ)是我們的擬合函數

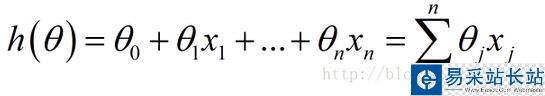
也可以用向量的形式進行表示：

下面函數是我們需要進行最優化的風險函數，其中的每一項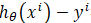都表示在已有的訓練集上我們的擬合函數與y之間的殘差，計算其平方損失函數作為我們構建的風險函數（參見最小二乘法及其Python實現）

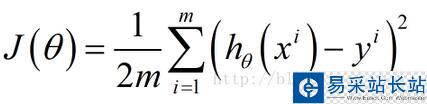
這里我們乘上1/2是為了方便后面求偏導數時結果更加簡潔，之所以能乘上1/2是因為乘上這個系數后對求解風險函數最優值沒有影響。

我們的目標就是要最小化風險函數，使得我們的擬合函數能夠最大程度的對目標函數y進行擬合，即：

后面的具體梯度求解都是圍繞這個目標來進行。

批量梯度下降BGD

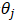按照傳統的思想，我們需要對上述風險函數中的每個求其偏導數，得到每個對應的梯度

這里表示第i個樣本點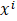的第j分量，即h(θ)中的