蒙特卡羅方法是一種統(tǒng)計模擬方法，由馮·諾依曼和烏拉姆提出，在大量的隨機數(shù)下，根據(jù)概率估計結果，隨機數(shù)據(jù)越多，獲得的結果越精確。下面我們將用python實現(xiàn)蒙特卡羅方法。

1.首先我們做一個簡單的圓周率的近似計算，在這個過程中我們要用到隨機數(shù)，因此需要先使用import numpy as np導入numpy庫。

2.代碼實現(xiàn)：

import numpy as np total = 8000000count = 0 for i in range(total): x = np.random.rand() y = np.random.rand() dis = (x**2+y**2)**0.5 if dis <= 1:  count = count+1PI = 4*count/totalprint(PI)

3.在上面的程序中我們用8000000個隨機數(shù)進行投放，這樣得到的結果會更精確一些，運行程序需要一定的時間，最終得到的結果如下

4.下面我們進行一項簡單的應用，下圖為我在畫圖工具中隨便畫的一個圖，我們可以用蒙特卡羅方法來估算圖中黑色部分的面積。

5.上面的圖形是不規(guī)則的，我們只需知道在投放大量隨機數(shù)的情況下，隨機數(shù)在黑色部分出現(xiàn)的概率，再用總面積相乘即可估算黑色部分的面積。我們知道，黑色的rgb編碼為(0,0,0)，所以需要統(tǒng)計rgb編碼為(0,0,0)時隨機數(shù)的投放概率即可。

6.代碼實現(xiàn)：

from PIL import Imageimport numpy as np im = Image.open("C:/Users/21974/Desktop/handwrite2.PNG")total = 9000000count = 0defin = 0width = im.size[0]height = im.size[1] for i in range(total): #用蒙特卡羅方法獲得估計值 x = np.random.randint(0, width-1) y = np.random.randint(0, height-1) k = im.getpixel((x, y)) if k[0]+k[1]+k[2] == 0:  count += 1print(int(width*height*count/total)) for i in range(width): #用遍歷獲得準確值 for j in range(height):  k = im.getpixel((i, j))  if k[0] + k[1] + k[2] == 0:   defin += 1print(defin)

上面的代碼可分為兩部分，第一個for后面是用蒙特卡羅方法獲得的面積的估計值，第二個for后面是用遍歷所有像素點的方法獲得的面積的精確值，獲得兩個輸出后進行對比。

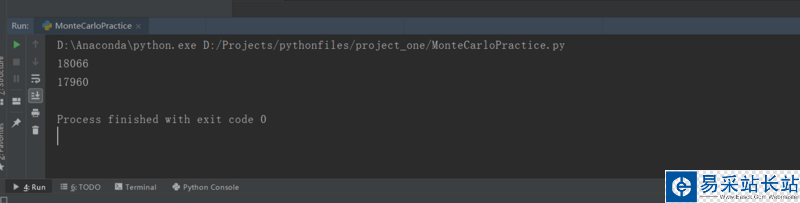
我們在上面的程序中采用了9000000個隨機數(shù)，可以看出兩個輸出結果相差并不大。