這個(gè)階段一直在做和梯度一類算法相關(guān)的東西，索性在這兒做個(gè)匯總，

一、算法論述

梯度下降法(gradient  descent)別名最速下降法（曾經(jīng)我以為這是兩個(gè)不同的算法-.-）,是用來求解無約束最優(yōu)化問題的一種常用算法。下面以求解線性回歸為題來敘述：

設(shè)：一般的線性回歸方程（擬合函數(shù)）為：（其中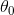的值為1）

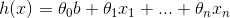
則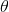這一組向量參數(shù)選擇的好與壞就需要一個(gè)機(jī)制來評(píng)估，據(jù)此我們提出了其損失函數(shù)為(選擇均方誤差)：

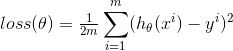
我們現(xiàn)在的目的就是使得損失函數(shù)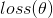取得最小值，即目標(biāo)函數(shù)為：

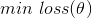
如果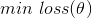的值取到了0，意味著我們構(gòu)造出了極好的擬合函數(shù)，也即選擇出了最好的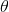值，但這基本是達(dá)不到的，我們只能使得其無限的接近于0，當(dāng)滿足一定精度時(shí)停止迭代。

那么問題來了如何調(diào)整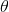使得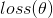取得的值越來越小呢？方法很多，此處以梯度下降法為例：

分為兩步：（1）初始化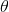的值。

                  （2）改變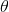的值，使得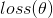按梯度下降的方向減少。

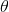值的更新使用如下的方式來完成：

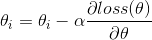
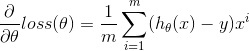
其中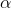為步長因子，這里我們?nèi)《ㄖ担⒁馊绻?img alt="" src="/d/file/p/2020/02-16/47215caabaf188cb4f0e6d41813e7261.gif" />取得過小會(huì)導(dǎo)致收斂速度過慢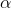，過大則損失函數(shù)可能不會(huì)收斂，甚至逐漸變大，可以在下述的代碼中修改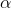的值來進(jìn)行驗(yàn)證。后面我會(huì)再寫一篇關(guān)于隨機(jī)梯度下降法的文章，其實(shí)與梯度下降法最大的不同就在于一個(gè)求和符號(hào)。