本文實例講述了Python基于最小二乘法實現曲線擬合。分享給大家供大家參考，具體如下：

這里不手動實現最小二乘，調用scipy庫中實現好的相關優化函數。

考慮如下的含有4個參數的函數式：

構造數據

import numpy as npfrom scipy import optimizeimport matplotlib.pyplot as pltdef logistic4(x, A, B, C, D):  return (A-D)/(1+(x/C)**B)+Ddef residuals(p, y, x):  A, B, C, D = p  return y - logisctic4(x, A, B, C, D)def peval(x, p):  A, B, C, D = p  return logistic4(x, A, B, C, D)A, B, C, D = .5, 2.5, 8, 7.3x = np.linspace(0, 20, 20)y_true = logistic4(x, A, B, C, D)y_meas = y_true + 0.2 * np.random.randn(len(y_true))

調用工具箱函數，進行優化

p0 = [1/2]*4plesq = optimize.leastsq(residuals, p0, args=(y_meas, x))            # leastsq函數的功能其實是根據誤差（y_meas-y_true）            # 估計模型（也即函數）的參數

繪圖

plt.figure(figsize=(6, 4.5))plt.plot(x, peval(x, plesq[0]), x, y_meas, 'o', x, y_true)plt.legend(['Fit', 'Noisy', 'True'], loc='upper left')plt.title('least square for the noisy data (measurements)')for i, (param, true, est) in enumerate(zip('ABCD', [A, B, C, D], plesq[0])):  plt.text(11, 2-i*.5, '{} = {:.2f}, est({:.2f}) = {:.2f}'.format(param, true, param, est))plt.savefig('./logisitic.png')plt.show()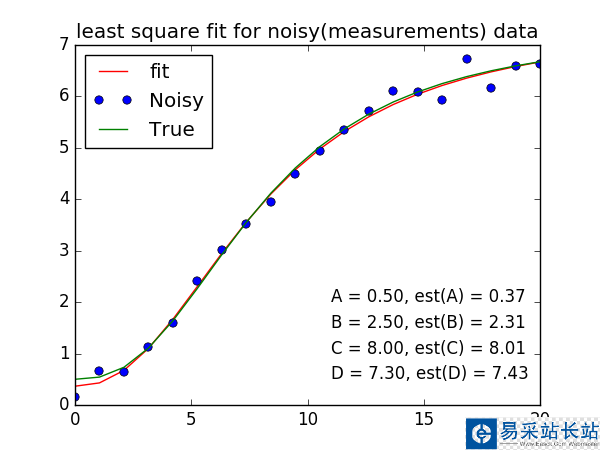

PS：這里再為大家推薦兩款相似的在線工具供大家參考：

在線多項式曲線及曲線函數擬合工具：
http://tools.jb51.net/jisuanqi/create_fun

在線繪制多項式/函數曲線圖形工具：
http://tools.jb51.net/jisuanqi/fun_draw

更多關于Python相關內容感興趣的讀者可查看本站專題：《Python數學運算技巧總結》、《Python數據結構與算法教程》、《Python函數使用技巧總結》、《Python字符串操作技巧匯總》及《Python入門與進階經典教程》

希望本文所述對大家Python程序設計有所幫助。