Tensorflow二維、三維、四維矩陣運算（矩陣相乘，點乘，行/列累加）

1. 矩陣相乘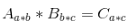

根據(jù)矩陣相乘的匹配原則，左乘矩陣的列數(shù)要等于右乘矩陣的行數(shù)。

在多維（三維、四維）矩陣的相乘中，需要最后兩維滿足匹配原則。

可以將多維矩陣理解成：（矩陣排列，矩陣），即后兩維為矩陣，前面的維度為矩陣的排列。

比如對于（2，2，4）來說，視為2個（2，4）矩陣。

對于（2，2，2，4）來說，視為2*2個（2，4）矩陣。

import tensorflow as tf a_2d = tf.constant([1]*6, shape=[2, 3])b_2d = tf.constant([2]*12, shape=[3, 4])c_2d = tf.matmul(a_2d, b_2d)a_3d = tf.constant([1]*12, shape=[2, 2, 3])b_3d = tf.constant([2]*24, shape=[2, 3, 4])c_3d = tf.matmul(a_3d, b_3d)a_4d = tf.constant([1]*24, shape=[2, 2, 2, 3])b_4d = tf.constant([2]*48, shape=[2, 2, 3, 4])c_4d = tf.matmul(a_4d, b_4d) with tf.Session() as sess: tf.global_variables_initializer().run() print("# {}*{}={} /n{}".  format(a_2d.eval().shape, b_2d.eval().shape, c_2d.eval().shape, c_2d.eval())) print("# {}*{}={} /n{}".  format(a_3d.eval().shape, b_3d.eval().shape, c_3d.eval().shape, c_3d.eval())) print("# {}*{}={} /n{}".  format(a_4d.eval().shape, b_4d.eval().shape, c_4d.eval().shape, c_4d.eval()))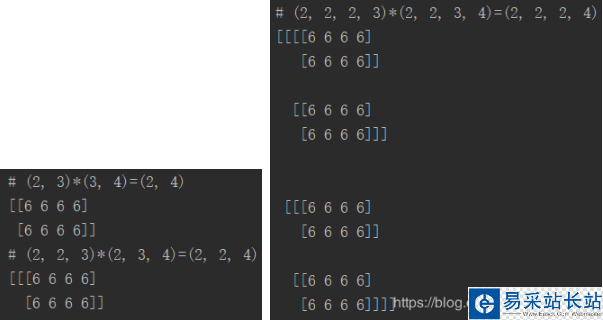

2. 點乘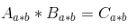

點乘指的是shape相同的兩個矩陣，對應(yīng)位置元素相乘，得到一個新的shape相同的矩陣。

a_2d = tf.constant([1]*6, shape=[2, 3])b_2d = tf.constant([2]*6, shape=[2, 3])c_2d = tf.multiply(a_2d, b_2d)a_3d = tf.constant([1]*12, shape=[2, 2, 3])b_3d = tf.constant([2]*12, shape=[2, 2, 3])c_3d = tf.multiply(a_3d, b_3d)a_4d = tf.constant([1]*24, shape=[2, 2, 2, 3])b_4d = tf.constant([2]*24, shape=[2, 2, 2, 3])c_4d = tf.multiply(a_4d, b_4d)with tf.Session() as sess: tf.global_variables_initializer().run() print("# {}*{}={} /n{}".  format(a_2d.eval().shape, b_2d.eval().shape, c_2d.eval().shape, c_2d.eval())) print("# {}*{}={} /n{}".  format(a_3d.eval().shape, b_3d.eval().shape, c_3d.eval().shape, c_3d.eval())) print("# {}*{}={} /n{}".  format(a_4d.eval().shape, b_4d.eval().shape, c_4d.eval().shape, c_4d.eval()))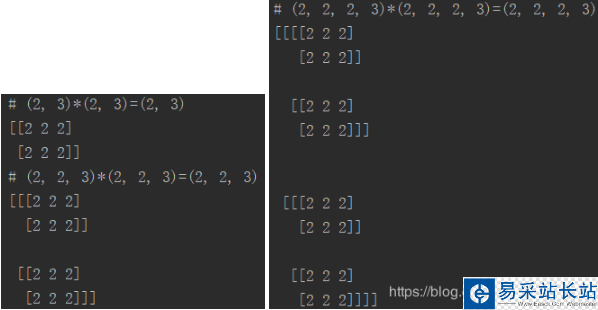

另外，點乘的其中一方可以是一個常數(shù)，也可以是一個和矩陣行向量等長（即列數(shù)）的向量。

即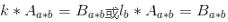

因為在點乘過程中，會自動將常數(shù)或者向量進行擴維。

a_2d = tf.constant([1]*6, shape=[2, 3])k = tf.constant(2)l = tf.constant([2, 3, 4])b_2d_1 = tf.multiply(k, a_2d) # tf.multiply(a_2d, k) is also okb_2d_2 = tf.multiply(l, a_2d) # tf.multiply(a_2d, l) is also oka_3d = tf.constant([1]*12, shape=[2, 2, 3])b_3d_1 = tf.multiply(k, a_3d) # tf.multiply(a_3d, k) is also okb_3d_2 = tf.multiply(l, a_3d) # tf.multiply(a_3d, l) is also oka_4d = tf.constant([1]*24, shape=[2, 2, 2, 3])b_4d_1 = tf.multiply(k, a_4d) # tf.multiply(a_4d, k) is also okb_4d_2 = tf.multiply(l, a_4d) # tf.multiply(a_4d, l) is also ok with tf.Session() as sess: tf.global_variables_initializer().run() print("# {}*{}={} /n{}".  format(k.eval().shape, a_2d.eval().shape, b_2d_1.eval().shape, b_2d_1.eval())) print("# {}*{}={} /n{}".  format(l.eval().shape, a_2d.eval().shape, b_2d_2.eval().shape, b_2d_2.eval())) print("# {}*{}={} /n{}".  format(k.eval().shape, a_3d.eval().shape, b_3d_1.eval().shape, b_3d_1.eval())) print("# {}*{}={} /n{}".  format(l.eval().shape, a_3d.eval().shape, b_3d_2.eval().shape, b_3d_2.eval())) print("# {}*{}={} /n{}".  format(k.eval().shape, a_4d.eval().shape, b_4d_1.eval().shape, b_4d_1.eval())) print("# {}*{}={} /n{}".  format(l.eval().shape, a_4d.eval().shape, b_4d_2.eval().shape, b_4d_2.eval()))