前言:
android/197674.html">貝塞爾曲線又稱貝茲曲線,它的主要意義在于無論是直線或曲線都能在數學上予以描述。最初由保羅·德卡斯特里奧(Paul de Casteljau)于1959年運用德卡斯特里奧演算法開發(de Casteljau Algorithm),在1962,由法國工程師皮埃爾·貝塞爾(Pierre Bézier)所廣泛發表。目前廣泛應用于圖形繪制領域來模擬光滑曲線,為計算機矢量圖形學奠定了基礎。在一些圖形處理軟件中都能見到貝塞爾曲線,比如CorelDraw中翻譯成“貝賽爾工具”;而在Fireworks中叫“畫筆”;Photoshop中叫“鋼筆工具”。下圖為Photoshop中用鋼筆繪制的貝塞爾曲線,共繪制了三條貝塞爾曲線:

數學表達
術語:數據點、控制線、控制點、德卡斯特里奧算法、一階,二階,三階,n階……
一階貝塞爾曲線示意圖
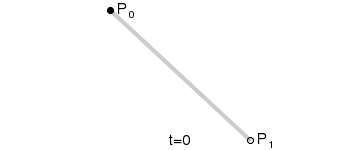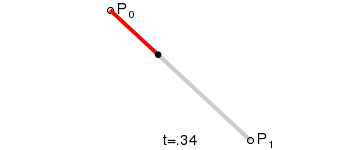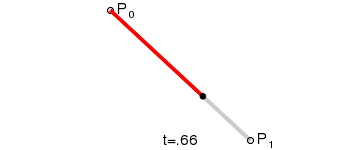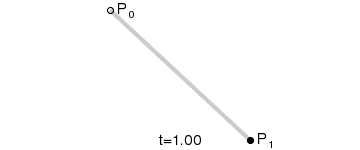
一階貝塞爾曲線公式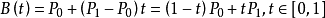
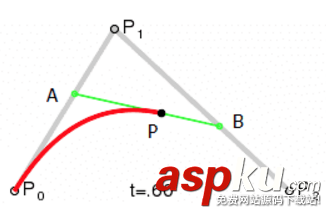
二階貝塞爾曲線:圖中第二段為二階貝塞爾曲線,只有一個控制點,即只有一個控制點和兩個數據點來決定曲線形狀。
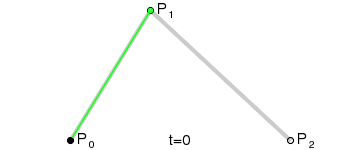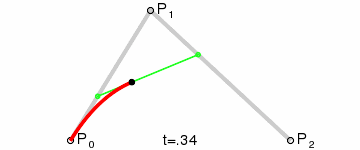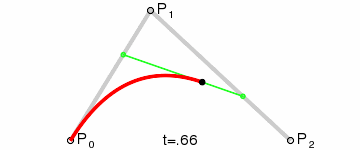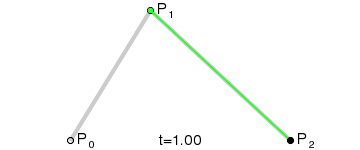
二階貝塞爾曲線公式
二階公式推導:
二階貝塞爾曲線t=0.6示意圖.gif
根據控制點和數據點,對貝塞爾曲線進行約束,滿足的條件為
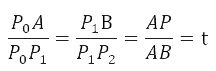
問題變為:已知P0(x0,y0), P1(x1,y1), P2(x2,y2),根據上式求P點坐標?
先求出A、B點坐標,其坐標
PA=P0+(P1-P0)·t
PB=P1+(P2-P1)·t
之后求P點坐標,其坐標
P=PA+(PB-PA)·t
P=(1-t)2P0+2t(1-t)P1+t2P2, t∈[0,1]
三階貝塞爾曲線:圖中第三段為三階貝塞爾曲線,有兩個控制點和兩個數據點決定的曲線,同樣滿足等比條件:
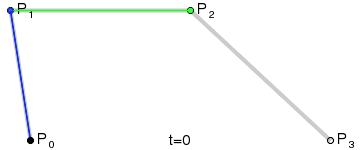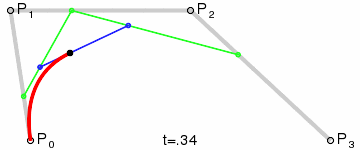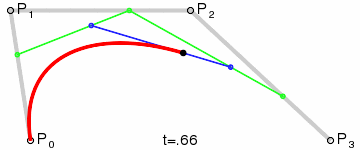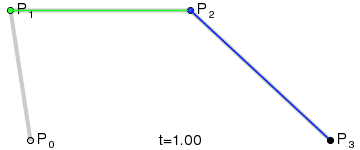
三階貝塞爾曲線
三階貝塞爾曲線公式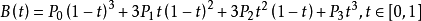
德卡斯特里奧算法的思想:給定數據點和控制點P0、P1…Pn,首先將數據點和控制點連接形成一條折線,計算出每條折線上面的一點,使得初始數據點(初始控制點)到該點的距離與初始數據點(初始控制點)到終止數據點(終止控制點)的距離之比為t:1。將這些點連接起來形成新的折線(折線少了一段),用遞歸的算法繼續計算,指導只有兩個點,在這兩個點形成的線段上去一點,滿足以上的比例關系。隨著t的從0到1的變化,該點的集合形成了貝塞爾曲線。
n階貝塞爾曲線公式如下。
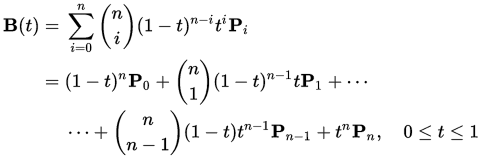
Android中的應用
對android中如何獲取貝塞爾曲線上的點,如何繪制貝塞爾曲線,以及結合貝塞爾曲線的知識做出的效果進行分析。
1. 獲取貝塞爾曲線上點的坐標
在android中并沒有直接獲取的方法,因此需要利用上面的公式進行計算,以二階貝塞爾曲線為例,獲取51個點,主要是t從0開始到1間取51項的等差數列:
public class MainActivity extends AppCompatActivity { private static final float mPointNum = 50f; @Override protected void onCreate(Bundle savedInstanceState) { super.onCreate(savedInstanceState); setContentView(R.layout.activity_main); init(); } private void init() { PointF mStartPoint = new PointF(0, 0); PointF mEndPoint = new PointF(0, 1200); PointF mControlPoint = new PointF(500, 600); List<PointF> mPointList = new ArrayList<>(); for (int i = 0; i <= mPointNum; i++) { mPointList.add(getBezierPoint(mStartPoint, mEndPoint, mControlPoint, i / mPointNum)); Log.d("Bezier", "X:" + mPointList.get(i).x + " Y:" + mPointList.get(i).y); } } private PointF getBezierPoint(PointF start, PointF end, PointF control, float t) { PointF bezierPoint = new PointF(); bezierPoint.x = (1 - t) * (1 - t) * start.x + 2 * t * (1 - t) * control.x + t * t * end.x; bezierPoint.y = (1 - t) * (1 - t) * start.y + 2 * t * (1 - t) * control.y + t * t * end.y; return bezierPoint; }}如果需要更高階,可以使用遞歸函數來運算
//用遞歸獲取貝塞爾曲線點的x軸坐標private float getBezierPointX(int n, int position, float t) { if (n == 1) { return (1 - t) * mPointList.get(position).x + t * mPointList.get(position + 1).x; } return (1 - t) * getBezierPointX(n - 1, position, t) + t * getBezierPointX(n - 1, position + 1, t); }//用遞歸獲取貝塞爾曲線點的x軸坐標private float getBezierPointX(int n, int position, float t) { if (n == 1) { return (1 - t) * mPointList.get(position).x + t * mPointList.get(position + 1).x; } return (1 - t) * getBezierPointX(n - 1, position, t) + t * getBezierPointX(n - 1, position + 1, t); }private ArrayList<PointF> buildBezierPoints() { ArrayList<PointF> points = new ArrayList<>(); int order = mPointList.size() - 1; float delta = 1.0f / POINT_NUM; for (float t = 0; t <= 1; t += delta) { // Bezier點集 points.add(new PointF(getBezierPointX(order, 0, t), getBezierPointY(order, 0, t))); } return points; }2. 繪制貝塞爾曲線
Android 中的Path類可以直接繪制一階到三階的貝塞爾曲線,在onDraw(Canvas canvas) 方法中使用:
繪制一階貝塞爾曲線:
canvas.drawLine(start.x,start.y,end.x,end.y);
繪制二階貝塞爾曲線:
mPath.moveTo(startPoint.x, startPoint.y);//起點mPath.quadTo(controlPoint1.x, controlPoint1.y, endPoint.x, endPoint.y);canvas.drawPath(mPath, mPaint);
繪制三階貝塞爾曲線:
mPath.moveTo(startPoint.x, startPoint.y);//起點mPath.cubicTo(controlPoint1.x, controlPoint1.y, controlPoint2.x, controlPoint2.y, endPoint.x, endPoint.y);canvas.drawPath(mPath, mPaint);
繪制n階貝塞爾曲線
n階貝塞爾曲線繪制,需要結合遞歸函數,設定一條曲線由多少個點組成,通過循環獲取每個點的坐標進行繪制。

7階貝塞爾曲線

8階貝塞爾曲線
3.Demo
貝塞爾曲線在android中最常用的是做出一些動畫特效,如QQ消息數拖拽形變效果,一些炫酷的下拉刷新控件,閱讀軟件的翻書效果,一些平滑的折線圖的制作,某圖片的運動軌跡等……
3.1 形狀變形
只需要知道變形前和變形后圖形的數據點和控制點即可,通過改變數據點和控制點使得形狀發生改變。

初始化
private float[] mData = new float[8]; // 順時針記錄繪制圓形的四個數據點 private float[] mCtrl = new float[16]; // 順時針記錄繪制圓形的八個控制點 private float mDuration = 1000; // 變化總時長 private float mCurrent = 0; // 當前已進行時長 private float mCount = 100; // 將時長總共劃分多少份 private float mPiece = mDuration / mCount; // 每一份的時長
在onDraw(Canvas canvas)方法中繪制
path.reset(); path.moveTo(mData[0], mData[1]); path.cubicTo(mCtrl[0], mCtrl[1], mCtrl[2], mCtrl[3], mData[2], mData[3]); path.cubicTo(mCtrl[4], mCtrl[5], mCtrl[6], mCtrl[7], mData[4], mData[5]); path.cubicTo(mCtrl[8], mCtrl[9], mCtrl[10], mCtrl[11], mData[6], mData[7]); path.cubicTo(mCtrl[12], mCtrl[13], mCtrl[14], mCtrl[15], mData[0], mData[1]); canvas.drawPath(path, mPaint); mCurrent += mPiece; if (mCurrent < mDuration) { mData[1] -= 120 / mCount; mCtrl[7] += 80 / mCount; mCtrl[9] += 80 / mCount; mCtrl[4] -= 20 / mCount; mCtrl[10] += 20 / mCount; postInvalidateDelayed((long) mPiece); }3.2 漂浮的愛心
愛心的漂浮軌跡就是一條三階貝塞爾曲線,結合屬性動畫中的估值器進行設置。
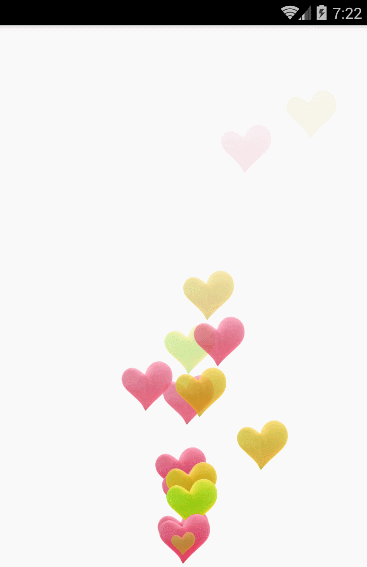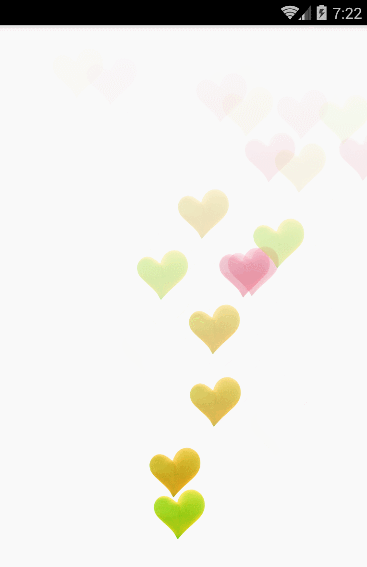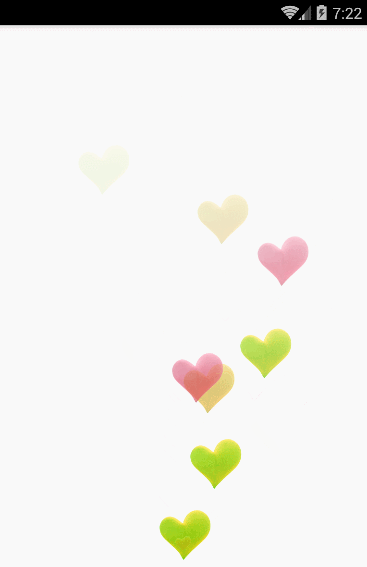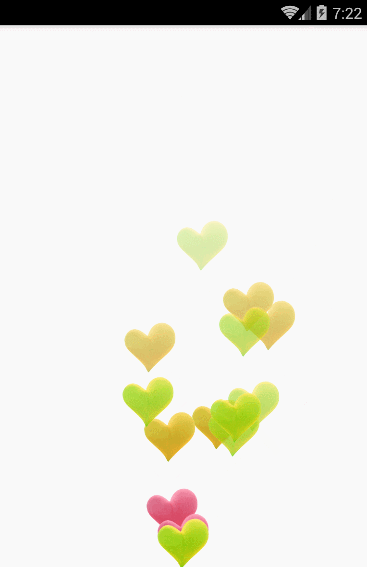
首先定義一個屬性動畫的估值器
public class BezierEvaluator implements TypeEvaluator<PointF> { private PointF mControlP1; private PointF mControlP2; public BezierEvaluator(PointF controlP1, PointF controlP2) { this.mControlP1 = controlP1; this.mControlP2 = controlP2; } @Override public PointF evaluate(float time, PointF start, PointF end) { float timeLeft = 1.0f - time; PointF point = new PointF(); point.x = timeLeft * timeLeft * timeLeft * (start.x) + 3 * timeLeft * timeLeft * time * (mControlP1.x) + 3 * timeLeft * time * time * (mControlP2.x) + time * time * time * (end.x); point.y = timeLeft * timeLeft * timeLeft * (start.y) + 3 * timeLeft * timeLeft * time * (mControlP1.y) + 3 * timeLeft * time * time * (mControlP2.y) + time * time * time * (end.y); return point; }}之后自定義一個view可以生成愛心,添加透明度,縮放等動畫和根據貝塞爾曲線改變其位置的屬性動畫。
初始化愛心圖片和多個插值器等,到時隨即選取
private void init() { // 初始化顯示的圖片 drawables = new Drawable[3]; drawables[0] = getResources().getDrawable(R.drawable.red); drawables[1] = getResources().getDrawable(R.drawable.yellow); drawables[2] = getResources().getDrawable(R.drawable.green); // 初始化插補器 mInterpolators = new Interpolator[4]; mInterpolators[0] = new LinearInterpolator();// 線性 mInterpolators[1] = new AccelerateInterpolator();// 加速 mInterpolators[2] = new DecelerateInterpolator();// 減速 mInterpolators[3] = new AccelerateDecelerateInterpolator();// 先加速后減速 // 底部 并且 水平居中 dWidth = drawables[0].getIntrinsicWidth(); dHeight = drawables[0].getIntrinsicHeight(); lp = new LayoutParams(dWidth, dHeight); lp.addRule(CENTER_HORIZONTAL, TRUE);// 這里的TRUE 要注意 不是true lp.addRule(ALIGN_PARENT_BOTTOM, TRUE); }入場動畫
private AnimatorSet getEnterAnimator(final View target) { ObjectAnimator alpha = ObjectAnimator.ofFloat(target, View.ALPHA, 0.2f, 1f); ObjectAnimator scaleX = ObjectAnimator.ofFloat(target, View.SCALE_X, 0.2f, 1f); ObjectAnimator scaleY = ObjectAnimator.ofFloat(target, View.SCALE_Y, 0.2f, 1f); AnimatorSet enter = new AnimatorSet(); enter.setTarget(target); enter.setInterpolator(new LinearInterpolator()); enter.setDuration(500).playTogether(alpha, scaleX, scaleY); return enter; }貝塞爾曲線動畫
private ValueAnimator getBezierValueAnimator(final View target) { // 初始化貝塞爾估值器 BezierEvaluator evaluator = new BezierEvaluator(getPointF(2), getPointF(1)); // 起點在底部中心位置,終點在底部隨機一個位置 ValueAnimator animator = ValueAnimator.ofObject(evaluator, new PointF((mWidth - dWidth) / 2, mHeight - dHeight), new PointF(random.nextInt(getWidth()), 0)); animator.setTarget(target); animator.addUpdateListener(new ValueAnimator.AnimatorUpdateListener() { @Override public void onAnimationUpdate(ValueAnimator valueAnimator) { // 這里獲取到貝塞爾曲線計算出來的的x y值 賦值給view 這樣就能讓愛心隨著曲線走啦 PointF pointF = (PointF) valueAnimator.getAnimatedValue(); target.setX(pointF.x); target.setY(pointF.y); // alpha動畫 target.setAlpha(1 - valueAnimator.getAnimatedFraction()); } }); animator.setDuration(3000); return animator; }結合動畫添加愛心
public void addHeart() { final ImageView imageView = new ImageView(getContext()); // 隨機選一個愛心 imageView.setImageDrawable(drawables[random.nextInt(3)]); imageView.setLayoutParams(lp); addView(imageView); AnimatorSet finalSet = new AnimatorSet(); AnimatorSet enterAnimatorSet = getEnterAnimator(imageView);//入場動畫 ValueAnimator bezierValueAnimator = getBezierValueAnimator(imageView);//貝塞爾曲線路徑動畫 finalSet.playSequentially(enterAnimatorSet, bezierValueAnimator); finalSet.setInterpolator(mInterpolators[random.nextInt(4)]); finalSet.setTarget(imageView); finalSet.addListener(new AnimatorListenerAdapter() { @Override public void onAnimationEnd(Animator animation) { super.onAnimationEnd(animation); removeView((imageView));//刪除愛心 } }); finalSet.start(); }3.3 貝塞爾曲線側邊索引條
實例地址:FancyListIndexer.rar
以上就是本文的全部內容,希望對大家的學習有所幫助,也希望大家多多支持VEVB武林網。
新聞熱點
疑難解答