幾何平均數(shù)是n個變量值連乘積的n次方根。

如果總水平、總成果等于所有階段、所有環(huán)節(jié)水平、成果的連乘積總和時，求各階段、各環(huán)節(jié)的一般水平、一般成果，要使用幾何平均法計算幾何平均數(shù)。

其特點包括：

（1）幾何平均數(shù)受極端值的影響較算術(shù)平均數(shù)小；

（2）如果變量值有負(fù)值，計算出的幾何平均數(shù)就會成為負(fù)數(shù)或虛數(shù)；

（3）它僅適用于具有等比或近似等比關(guān)系的數(shù)據(jù)；

（4）幾何平均數(shù)的對數(shù)是各變量值對數(shù)的算術(shù)平均數(shù)。

要注意的是變量數(shù)列中任何一個變量值不能為0，一個為0，則幾何平均數(shù)為0。

幾何平均數(shù)要求各觀察值之間存在連乘積關(guān)系，它的主要用途是：

（1）對比率、指數(shù)等進(jìn)行平均；

（2）計算平均發(fā)展速度；

（3）復(fù)利下的平均年利率；

（4）連續(xù)作業(yè)的車間求產(chǎn)品的平均合格率。

（以上內(nèi)容來自百度百科）

幾何平均數(shù)分為簡單幾何平均數(shù)和加權(quán)幾何平均數(shù)兩種。

（1）簡單幾何平均數(shù)

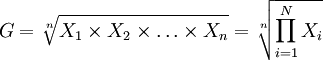
（2）加權(quán)幾何平均數(shù)

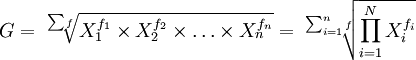
在R的基本函數(shù)中，沒有提供單獨計算幾何平均數(shù)的函數(shù)，但可以通過對算術(shù)平均數(shù)和加權(quán)平均數(shù)取對數(shù)，可以得到相應(yīng)的計算結(jié)果。

其原理比較簡單，假設(shè)這里求簡單幾何平均數(shù)，對公式兩側(cè)求自然對數(shù)，則有：

ln(G) = ln(X₁×X₂×...×X_n) /n =  [ln(X₁) + ln(X₂) + ... + ln(X_n)] / n

即，取自然對數(shù)后，相當(dāng)于對原變量的對數(shù)求算術(shù)平均值（在R中求算術(shù)平均值的介紹，請參見統(tǒng)計中集中趨勢的分析及在R語言中的計算）

則G = e^ln(G)

即求完原變量的自然對數(shù)的均值后，再計算以自然常數(shù)e為底，ln(G)為冪的值即可，這在R中可以輕松實現(xiàn)。

（1）例1 已知某市2010~2014年國內(nèi)生產(chǎn)總值的增長率（以上1年為1）分別為12%、8%、14%、16%和13%，試計算該市5年的平均增長率

編寫R程序：

x <- c(12,8,14,16,13)/100
tmp <- mean(log(1+x))
re <- exp(tmp) - 1
print(re)

計算結(jié)果為：0.1256843，即平均增長率為12.57%。

（2）例2 某銀行的某筆投資按復(fù)利計算，在11年中環(huán)比增長率：有3年為2%，5年4%，有1年為-2%，有2年為3%，請計算該銀行該筆投資年平均增長率。

編寫R程序：

x <- c(2,4,-2,3)/100
year <- c(3,5,1,2)
tmp <- weighted.mean(log(1+x),w=year)
re <- exp(tmp) - 1
print(re)

計算結(jié)果為：0.02712746，即該筆投資的年平均增長率為：2.71%。