人工神經網絡需要一定的數學基礎，但是一般來說比較簡單，簡單的高數基礎即可，這里整理了一些所需要的最基礎的概念的理解，對于神經網絡的入門，非常基礎和重要，而且理解了之后，會發(fā)現介紹不需要在看，磨刀不誤砍柴工，強烈建議理解清楚之后在去使用諸如tensorflow這樣的利器。

自變量/因變量/函數

因為E文文檔的閱讀時不可避免的接觸這些內容，一般將英文也列出來，盡量記住，閱讀時會大大提高速度。

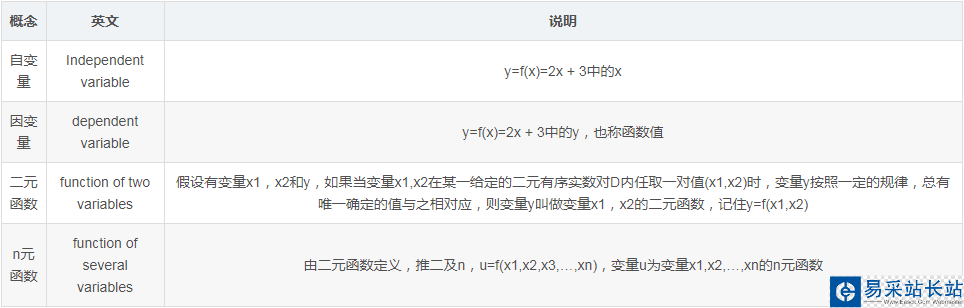
導數

作為高數最為基礎的導數概念，這里不在贅述，簡單烈一下內容能夠大體理解即可, 借用一張圖形來進行解釋： 

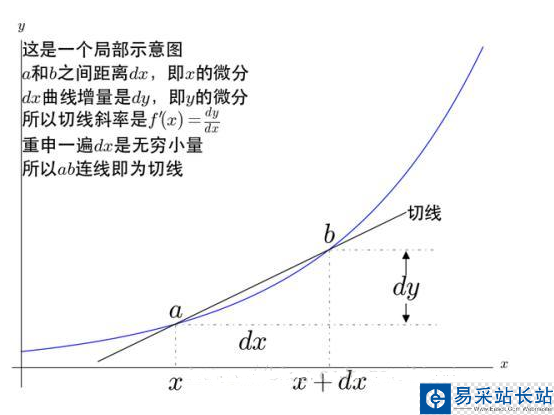
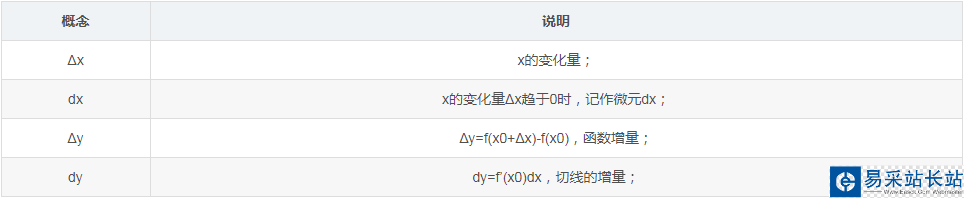
基本概念

導數/偏導數/方向導數/梯度，這四個概念無比重要，無比理解，簡單整理如下，比如在理解BP算法有所困難時請以此四概念為中心重新學習相關部分高數內容。

為何線性分類模型無法處理異或問題

異或是計算機中非常簡單的操作，而諸如感知機這樣的線性模型則無法解決異或問題的分類。嚴格的證明可以參看Minsky的文章。

簡單地來看，根據結果進行分類，可以分為兩類（0/1），但是如果顯示在一個平面上，你會發(fā)現無法找到一條直線將這兩類結果直接分開，所以可以直觀地看出是線性分類模型連異或這種簡單的分類都無法解決。

而這個悲傷的觀點，早在1969年Minsky就曾經在著名的Perceptron中已經被詳細地證明了，從而帶來了后來人工智能長達10年左右的冰凍期。這個問題并非無解，使用兩層的感知機即可解決這種問題，但是Minsky認為，這將會帶來巨大的計算量而且沒有有效的學習算法，直到諸如BP等算法的出現。1986年，Rumelhart，Geoffrey Hinton和Ronald Williams所發(fā)表的Learning representations by back-propagating errors一文中引入了BP算法到神經網絡模型之中，通過在神經網絡中添加隱含層，同時將誤差進行反向傳播，將糾錯的運算量下降到僅和神經元數目成正比的程度，解決了感知機的異或分類問題，同時為多層感知機的模型提供了學習算法。

回歸分析

在算法的入門時會學習使用線性回歸和邏輯回歸等，所以需要對回歸分析有一定的了解。回歸分析研究的是因變量和自變量之間的關系，在預測模型中被廣泛地應用。自變量的個數/因變量的類型/回歸線的形狀都是需要考慮的，常見的回歸分析方式如下：